【速さと比】同じ速さ・その5

この問題もとにかく解ければいいよ。
同一人物を２通りで見る、という解法にこだわらなくていいからね。

太郎がゴール（100ｍ）のとき、次郎は75ｍ進んだのだから、
２人の速さの比は、100:75=4：3　
太郎と次郎を「同じ時間」で比べました。

速さの比が、4：3である２人が、100ｍを走るのにかかる時間の比は３：４
太郎と次郎を「同じ距離」で比べました。

（速さ）×（時間）＝（距離）　
太郎：④×３秒＝100ｍ
次郎：③×４秒＝100ｍ

次郎が100ｍを走るのにかかる時間が、19秒とあるのだから、
４＝19

太郎が100ｍを走るのにかかる時間は３秒なので、太郎は１秒おくれてスタートすればよい。

19×\(\displaystyle \frac{1}{4}\) ＝\(\displaystyle \frac{19}{4}\) 秒だ。

\(\displaystyle \frac{19}{4}\) =4\(\displaystyle \frac{3}{4}\)秒遅れでスタートすればいいです！！

うん。お見事。
文句なしの正解だよ。

今回も、「同じ人を２通りで見る」ではなく解きましたけど。

そうだね。「同じ人を２通りで見る」解法も確認しておこうか。

太郎が100ｍ走る時間で、次郎は75ｍ走るから、
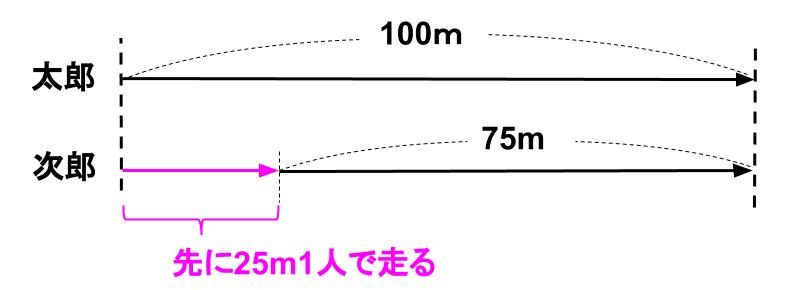
まず次郎だけ何秒間か１人で走らせて下図のようになればいいね。

なるほど、次郎が25ｍ走る時間だけ、太郎はスタートを遅らせればいいんだ。

次郎は100ｍを19秒だから、その \(\displaystyle \frac{1}{4}\) である25ｍを走るのにかかる時間は、\(\displaystyle \frac{19}{4}\) 秒か。

すっきり簡単ですね。

そういうことです。

様々な視点で考えることで、いろいろな問題に対する対応力がつくからね！