【速さと比】同じ速さ・その3

太郎くんは4400mを63分で進んでいますね。
午前９時から午前10時３分まで。

太郎の分速が求められますね。
4400÷63
割り切れないから分数か・・・ちょっといやだな。

そうだね。
太郎の速さは、分速 \(\displaystyle \frac{4400}{63}\) ｍ

この具体値を用いて解くこともできるけど、比を使ってさらっと解いてしまいましょう。
まずは図だね。

午前９時から午前９時36分までの36分間と、
午前９時36分から午前10時３分までの27分間に分けて考えます。
こんな感じですかね。

あれ？
これって、「同じ距離」タイプじゃないですか？
RQ間を、太郎は27分、次郎は36分で進んだ。
同じ距離を進むのにかかった時間の比が３：４だから、
２人の速さの比が逆比の４：３だってわかります。

そうだね。
それでも解けますよ。

速さ４の太郎が、ＰＱ間を63分かけて進んだのだから、
速さ３の次郎は、ＰＱ間を、

63×\(\displaystyle \frac{4}{3}\) =84

84分かけて進む。
次郎がＰ地点に着くのは、午前9時の84分後で、
午前10時24分です。
求まりました。

文句なしの正解です。

では、「同一人物（同じ速さ）の２通りに着目」で解いてみてください。
いろいろな視点を持っていると強いからね。

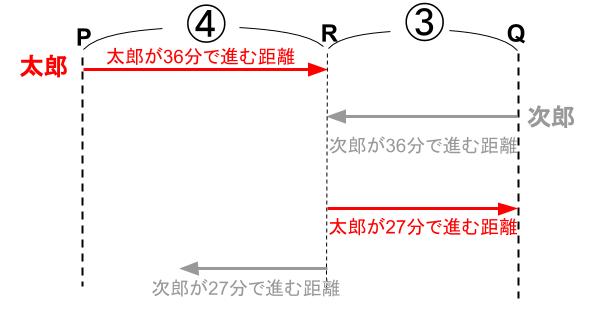
太郎ですね。
太郎が36分で進む距離と、27分で進む距離の比は、
36:27＝４：３

で、次郎に着目ですね。なるほど。

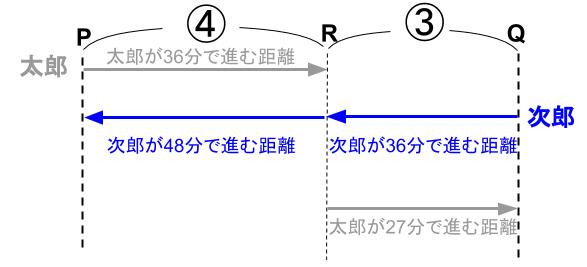
次郎が③の距離を進むのに36分かかるなら、
④の距離を進むのにかかる時間は

36× \(\displaystyle \frac{4}{3}\)=48（分）

午前9時36分の48分後は、午前10時24分

できましたよ。

カンペキですね。正解です。

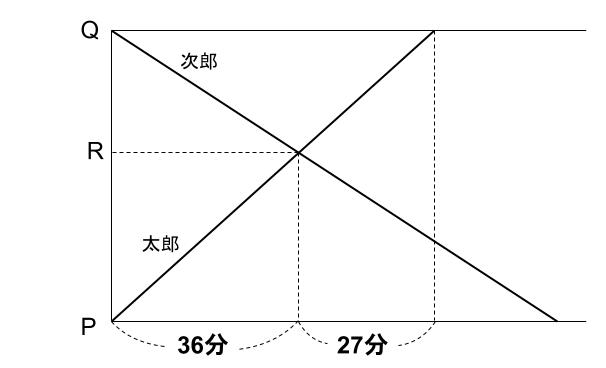
ちなみに、この問題は「同じ距離タイプ」でダイヤグラムで解いたこともあるよね。