3:4:5の直角三角形
7:24:25の直角三角形
例題1
3辺の長さが3cm、4cm、5cmの直角三角形6つを図のように並べるとき、次の各問いに答えよ。
(1)2点A,Bを直線で結ぶと、ABの長さは何cmか。
(2)2点CDを直線で結ぶと、CDの長さは何cmか。
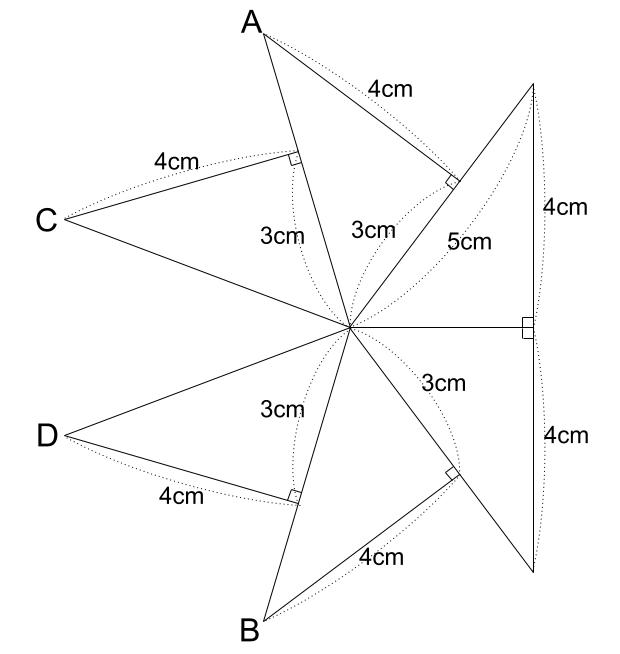
解説

灘中学で出題された問題です。
ABの真ん中の点をEとします。
下図のピンク色の直角三角形は特別なものです。
3辺の比が、7:24:25です。
角度からわかります。
青三角の角2つ分の外角だからです。

3:4:5の三角形の内角2つ分に注目するんでしたね。
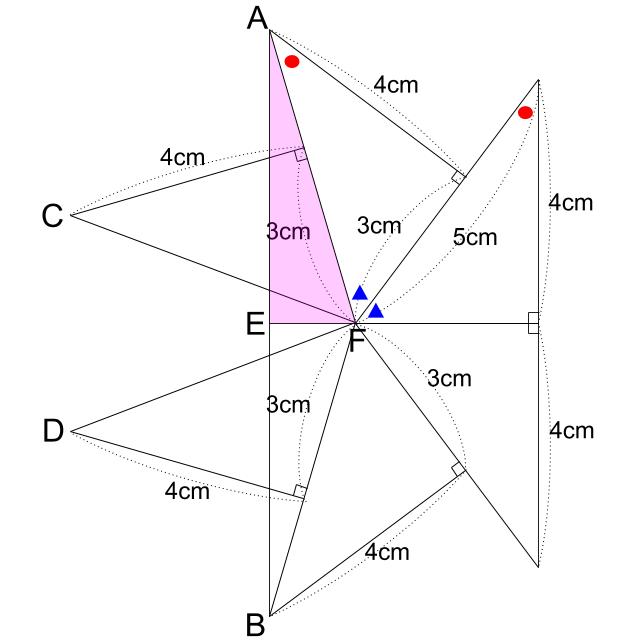

よって、AEの長さは、AFの長さの \(\displaystyle \frac{24}{25}\) 倍なので、
5× \(\displaystyle \frac{24}{25}\) = \(\displaystyle \frac{24}{5}\)
ABはAEの2倍なので、
\(\displaystyle \frac{24}{5}\) ×2= \(\displaystyle \frac{48}{5}\)=9.6
求まりました。
ABの長さは9.6cmです。
上の事実を暗記していない場合は、3:4:5の直角三角形を組み合わせたり、切ったりして解くことになります。
例えば、下図の直角三角形AEGは、3辺の比が3:4:5の直角三角形です。
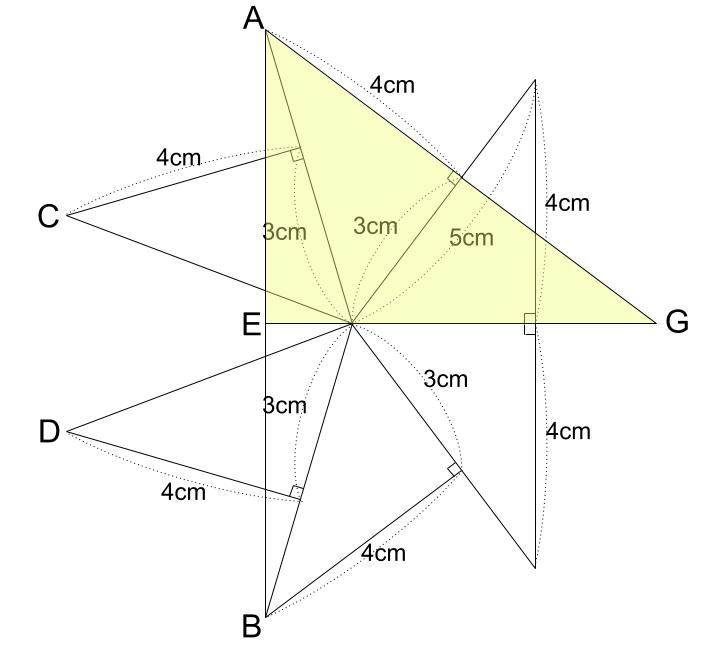

AEの長さは、AGの長さの \(\displaystyle \frac{3}{5}\) 倍なので、
8× \(\displaystyle \frac{3}{5}\) = \(\displaystyle \frac{24}{5}\)
\(\displaystyle \frac{24}{5}\) cmです。
このように解いている過程で、7:24:25に気づくこともあるでしょう。

続いてCDの長さです。
下図のピンク色の直角三角形CHIは、3辺の比が、7:24:25です。
角度からわかります。

赤丸2つ分の角があるからですね。
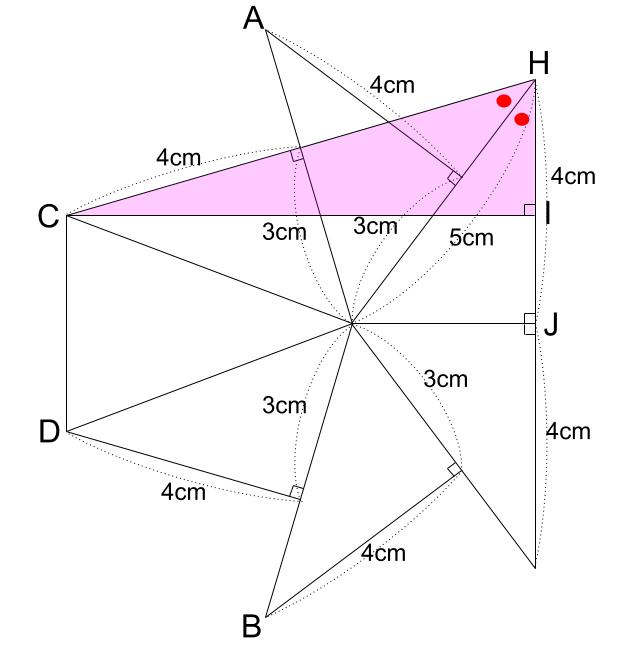

CH=8cmなので、
HI=8× \(\displaystyle \frac{7}{25}\) = \(\displaystyle \frac{56}{25}\)
\(\displaystyle \frac{56}{25}\) cmです。
より、IJ=4- \(\displaystyle \frac{56}{25}\) = \(\displaystyle \frac{44}{25}\)
CDはIJの2倍なので、
\(\displaystyle \frac{44}{25}\) ×2= \(\displaystyle \frac{88}{25}\) =3.52
求まりました。

この問題を、7:24:25の直角三角形の知識なしで解くのはかなり困難です。
様々な補助線を引いて、活路を見出すしかありません。
一例を示しておきます。
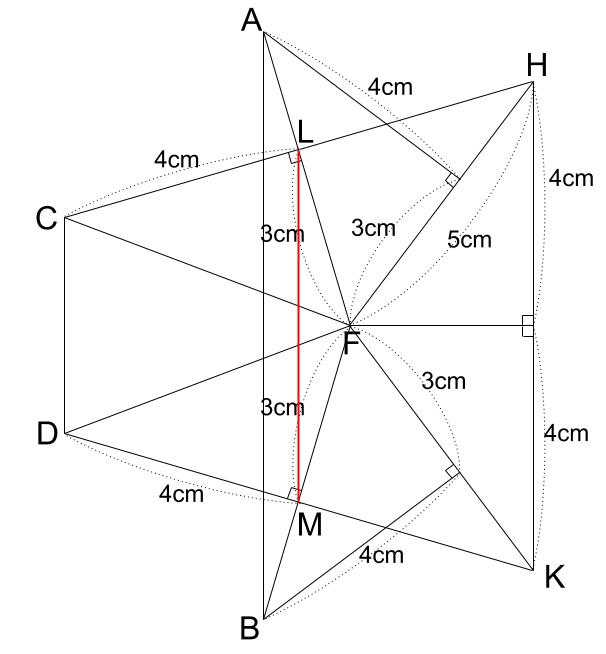

三角形FABと三角形FLMは相似で、相似比は、FA:FL=5:3なので、
LMはABの長さの\(\displaystyle \frac{3}{5}\)倍です。
ABは(1)より9.6cmなので、
LMは、9.6×\(\displaystyle \frac{3}{5}\)=5.76cm
また、CDの長さとHKの長さの平均がLMの長さになるので、
CDの長さが求まります。
(CD+8)×\(\displaystyle \frac{1}{2}\)=5.76
逆算して、CD=3.52
これで求まりました。
