3:4:5の直角三角形
7:24:25の直角三角形
例題1
下図のように長方形ABCDを対角線ACを折り目としておりました。
このとき、DEの長さを求めなさい。
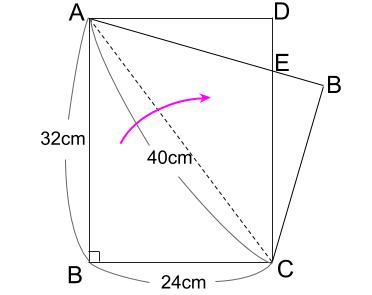
解説

折り返しの問題では、折り返す前と後で、同じものに着目する。
これが重要な解法知識です。
同じ長さや、同じ角度に着目するのです。
今回は、角度です。
角度から、直角三角形の相似がわかります。
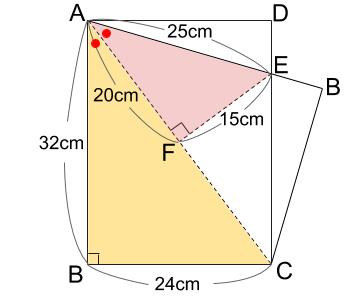

赤丸の角の大きさが等しいため、直角三角形ABCと直角三角形AFEは相似です。
どちらも、辺の長さの比が3:4:5の直角三角形です。
さらに、直角三角形AFEと直角三角形CFEは合同なので、EC=EA=25cm
より、DE=32-25=7(cm)
これが求める答えです。

なるほどー

ここからが本題になります!
この図形から学習したいことがあります。
ここで注目したいのは、直角三角形AEDです。
直角三角形AEDの辺の長さの比は7:24:25になることがわかりました。
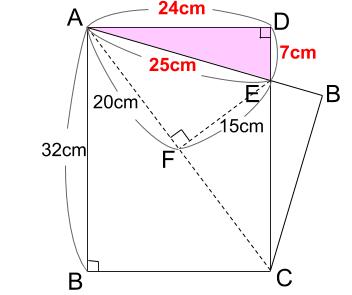

たしかに。
7cm,24cm,25cmですもんね。

このように直角三角形の3つの辺の比が、すべてが整数になることはめずらしいことです。
「3:4:5」だけでなく、この「7:24:25」も特別な三角形として暗記しておくと良いでしょう。
このように、3:4:5の直角三角形の問題に7:24:25の直角三角形はよく顔を出します。
覚えておいて損はありません。
どのような所に7:24:25の直角三角形が現れるか。
代表例は、上の例題でもでてきた配置です。


三角形ABC
三角形EBD
三角形EAD
がすべて「3:4:5」です。
そして、三角形AECが「7:24:25」
3:4:5の直角三角形の直角でない内角を上図のように、赤丸と青三角とします。
小さい方が赤丸で、大きい方が青三角です。
上図のように、赤丸2つ分の角は、7:24:25の直角三角形の1つの内角となります。
その角は、青三角2つ分の外角でもあります。

3:4:5の直角三角形の内角で、同じもの2つ分の角の大きさがあれば、7:24:25の直角三角形はあるということですね。

はい。そういうことです。
練習
下図において、2つの直角三角形は、いずれも3:4:5の直角三角形とします。
7:24:25の直角三角形がどこにあるか。見つけなさい。
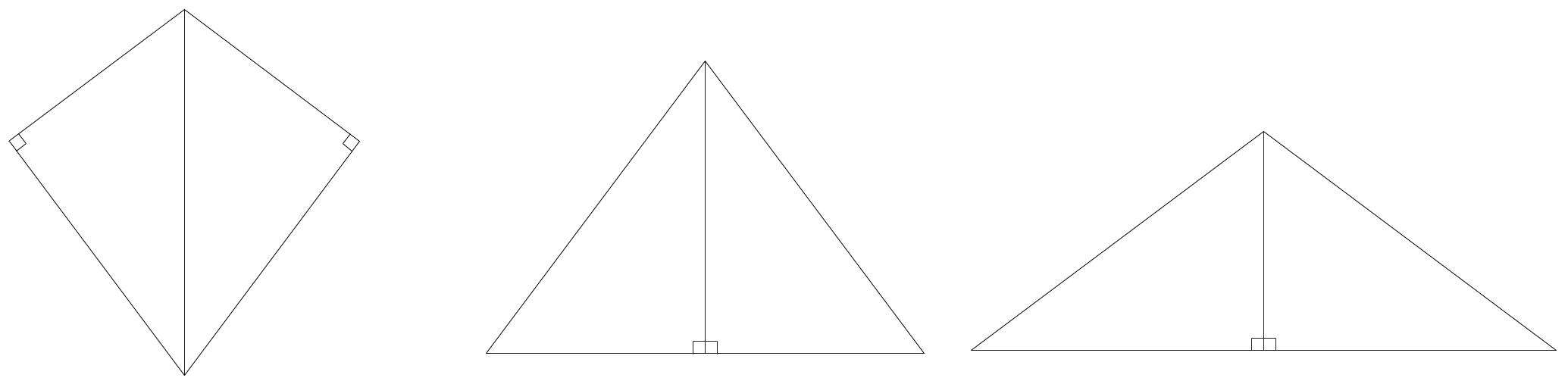
解説

例えば、下図のピンク色の直角三角形が7:24:25です。
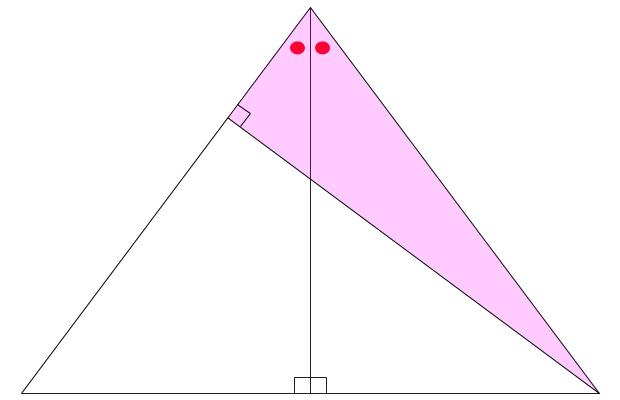

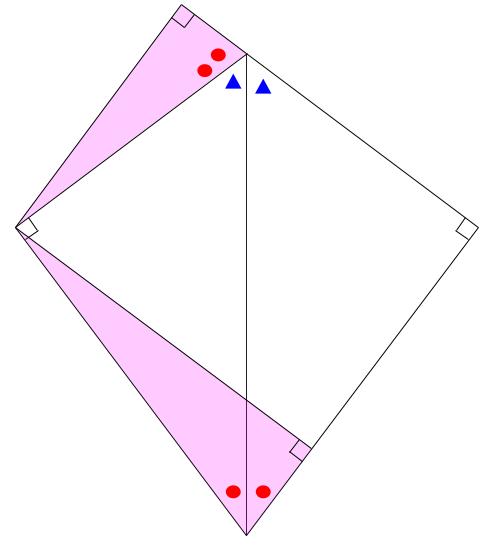

もちろん、対称な位置にも同様にあります。
