3:4:5の直角三角形
1:2と1:3の直角三角形
例題1
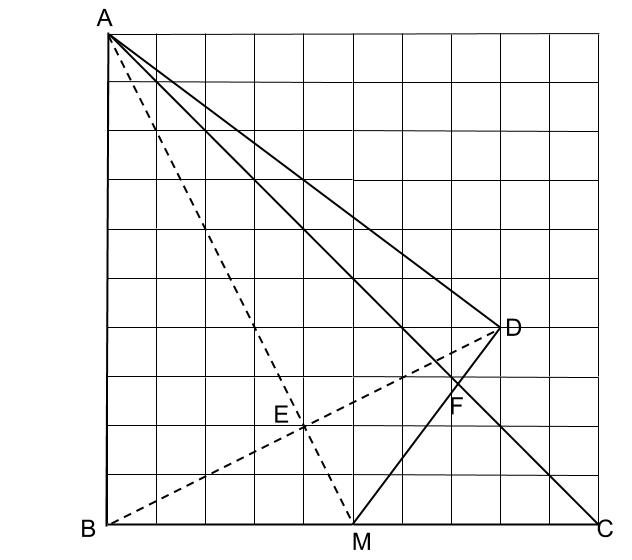
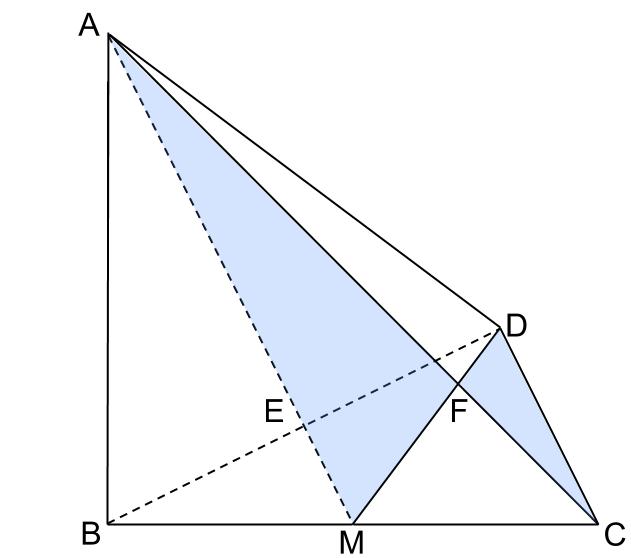
下の図で、三角形ABCは直角二等辺三角形で、AB、BCの長さは10cmです。辺BCのまん中の点をMとして、三角形ABMをAMで折り返してできる三角形がADMです。AMとBDの交点をE、ACとMDの交点をFとします。AEの長さはEMの長さの何倍ですか。
また、MFの長さは何cmですか。
解説

これは、平成23年の灘中学校で出題されました。
とても難しいのですが、やはり知識を使えば簡単に解決できます。
では、見ていきましょう。

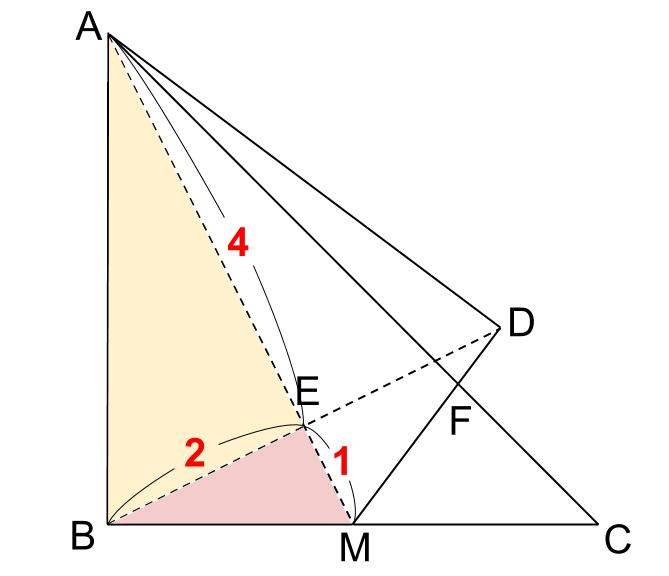
AE:EMは簡単ですね。
直角三角形の相似の定番の配置です。
下図のようになり、AE:EM=4:1と求まります。

三角形AMB
三角形ABE
三角形BME
これらがすべて「直角をはさむ辺の比が1:2の直角三角形」ですね。

続いて、MFの長さ。
これはかなりの難問です。
難しすぎるので、実入試においては捨てるの一手なんですけどね。
「直角をはさむ辺の比が1:2の直角三角形」に関する知識があれば・・・
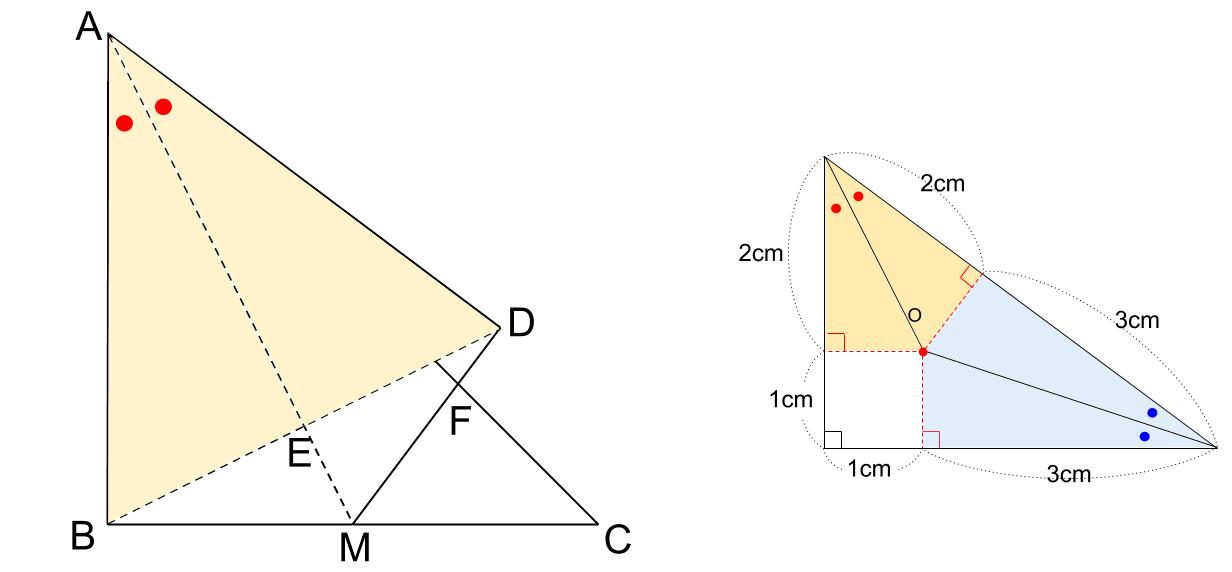

つまり、3:4:5の直角三角形が見つかります。
三角形APDがそれです。
下図のように長さの比が入ります。
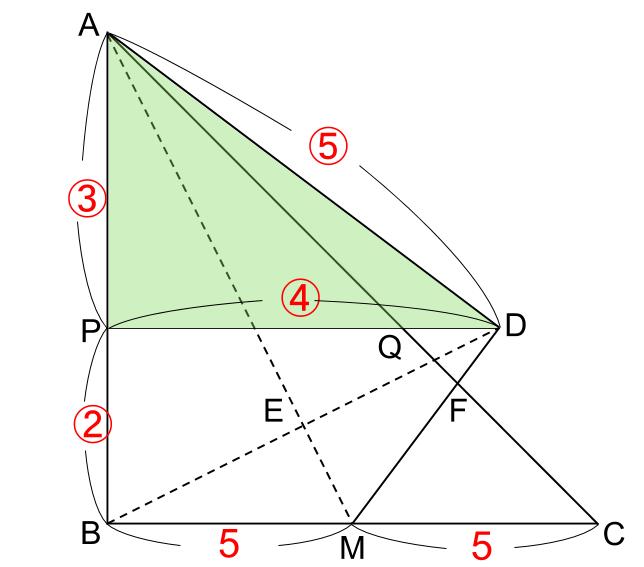

AB=AD=⑤=10cmなので、
①=2cm
下図のように長さが決まります。
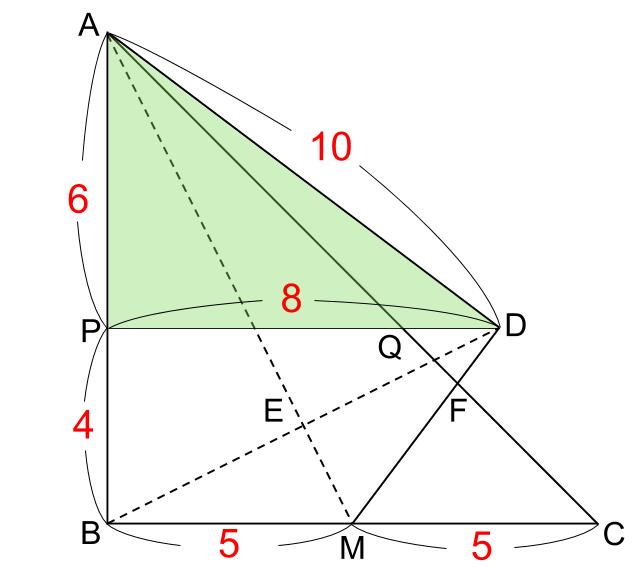

また、
直角二等辺三角形APQに着目して、
AP=PQ=6cm
なので、QD=8-6=2cm
MFの長さは、下図の砂時計相似から求まります。
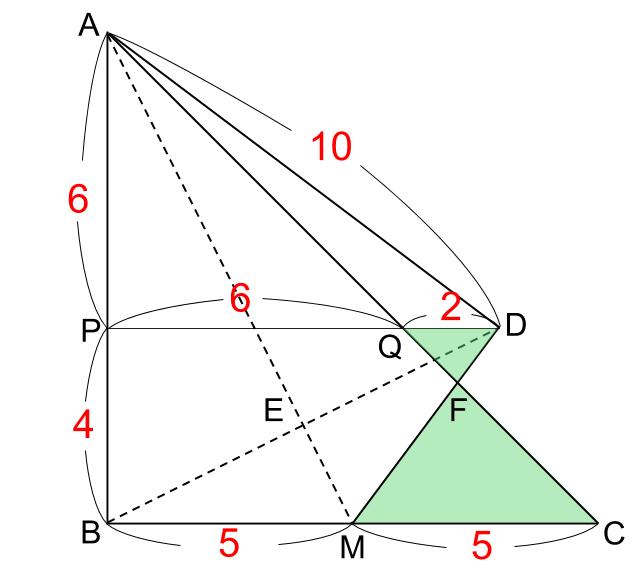

MF:DFは5:2なので、
MFはMDの \(\displaystyle \frac{5}{5+2}\) になります。
つまり、MD=5cmの \(\displaystyle \frac{5}{7}\) が求める長さです。
5×\(\displaystyle \frac{5}{7}\)=\(\displaystyle \frac{25}{7}\)
求まりました。

なるほど・・・
きれいに解けますね。
別解

あるいは、下の水色の三角形が直角をはさむ辺の比が1:3の直角三角形であるという知識を利用することもできます。
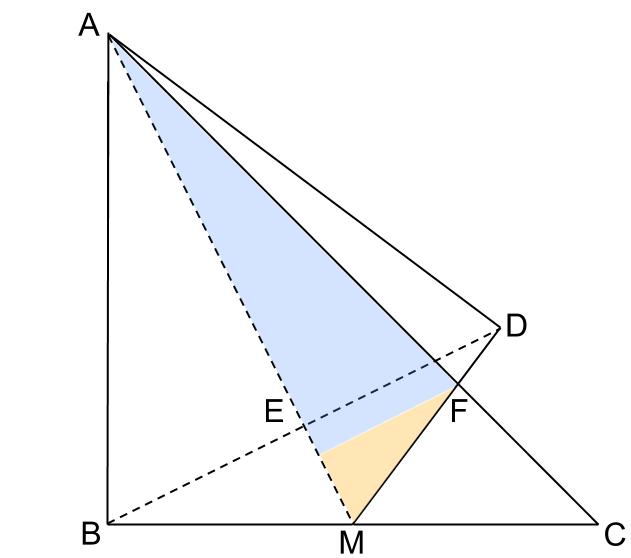

この問題を、これらの知識なしで解くのは至難です。
そのような解き方の一例を示すと、まずDCを結びます。
DCとAMが平行になることに気づかないと解けません。
二等辺三角形MDBと二等辺三角形MCDの内角から導かれます
(円周角の定理を知っていれば、Mを中心とする直径BCの円が想起されます)。
あとは砂時計相似です。
参考図