3:4:5の直角三角形
1:2と1:3の直角三角形
例題1
下図のように、横の長さが45cmの長方形を、DがBC上のEの位置にくるように折り返すとき、折れ線はAFとなります。このとき、BEの長さを求めなさい。
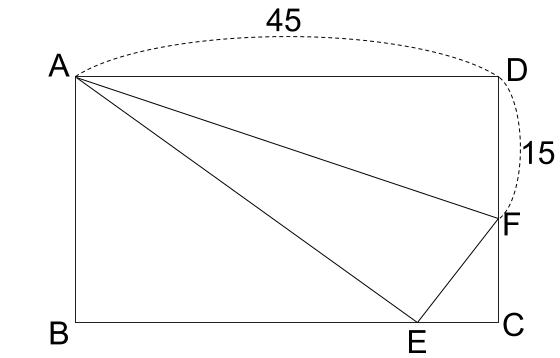
解説

「直角をはさむ辺の比が1:3の直角三角形」が2つあります。
3:4:5の直角三角形があるのは間違いないですね。
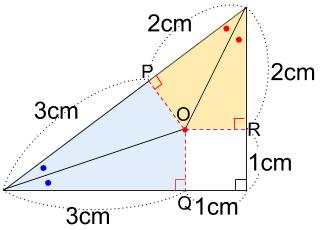

この知識があれば、直角三角形ABEや直角三角形ECFが3:4:5の直角三角形であることがわかります。

直角三角形ABEはAEが45cmです。
ADが折り返した移動先ですからね。
あとは辺の比が3:4:5なので、
AB=27cm
BE=36cm
ここまでくれば、ECやCFは引き算で求まります。
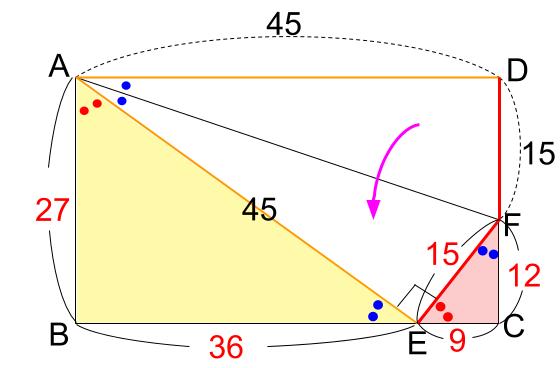

DFが折り返した移動先がEFですね。
DF=EF=15
直角三角形ECFも「3:4:5の直角三角形」になり、見事にぴったりです。
矛盾がありません。
これでうまくいっていることがわかります。
BEは36cmです。
別解

では、知識なしの正攻法でも解いておきましょう。
折り返しなので、
AEが45cm
EFが15cm
角AEFが90度がわかります。
また、角AEFが90度から、直角三角形ABEと直角三角形ECFが相似です。
角度から相似がわかります。
直角三角形の相似の有名な形ですよね。

丸と三角の角の和が90度ですね。
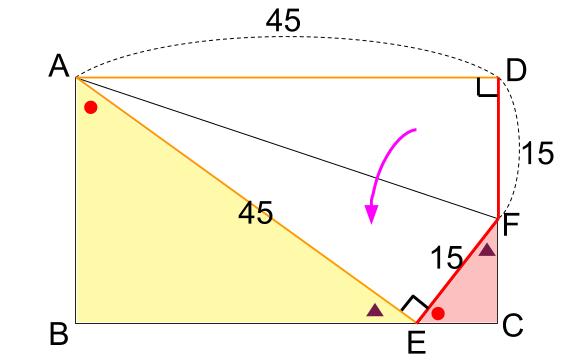

直角三角形ABEと直角三角形ECFの相似比は、45:15=3:1です。
つまり、下図のように長さの比が入ります。
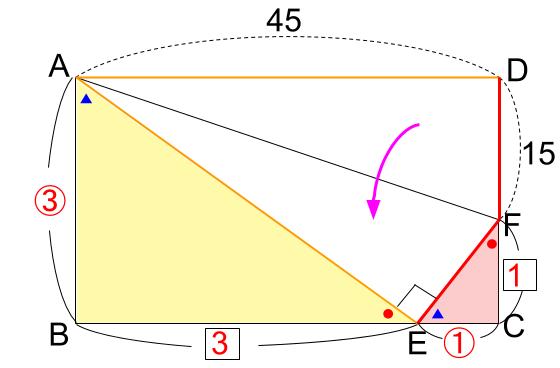

あとは消去算をすれば求まります。
DFとFCの和がABと等しいので、
15+1=③
BEとECの和がADと等しいので、
3+①=45
この2つの式で消去算をすると、
①=9
1=12
と求まります。
よって、BE=3=36
求まりました。
