3:4:5の直角三角形
1:2と1:3の直角三角形
例題1
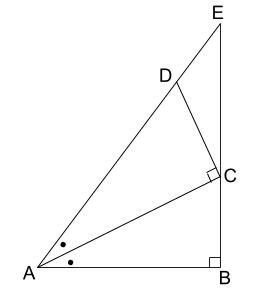
下図の三角形ABCの角Bと三角形ACDの角Cは直角で、●印がついた2つの角の大きさは等しいです。点Eは、辺BC、辺ADをそれぞれのばして交わった点です。辺ABの長さは2cmで、辺BCの長さは1cmです。
①三角形ACDの面積は何 \(cm^2\) ですか。
②CEの長さは何cmですか。
解説

これは、渋谷教育学園幕張中学で出題された問題です。
直角をはさむ辺の比が1:2の直角三角形がありますね。

はい、こんなときには、
3:4:5の直角三角形がかくれているかも、という目で問題を見てみます!
三角形EABが3:4:5の直角三角形に見えますね・・・

そうですね。
直角三角形EABは3:4:5の直角三角形に見えますね。
ところで、直角三角形EABの内角に、●が2つ分の角がありますね。
このことから、
直角三角形EABは「3:4:5の直角三角形である」と断定できます。
予想ではなくて、はっきりと確定できます。
下図の知識があれば。
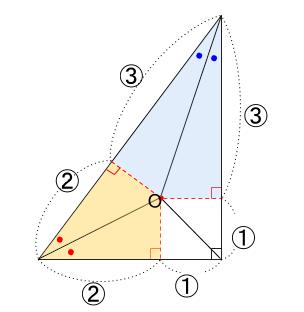

内接円のときに出てきた図ですね。

はい、そうです。
直角三角形EABが3:4:5の直角三角形であると分かれば・・・・
続きを解いてみてください。

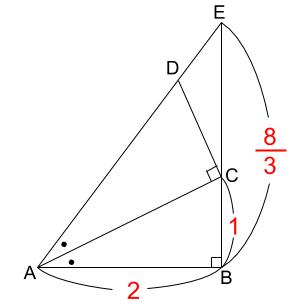
AB=2cmだから、
EBの長さは、2×\(\displaystyle \frac{4}{3}\)=\(\displaystyle \frac{8}{3}\)
BC=1cmなので、
EC=\(\displaystyle \frac{8}{3}\)-1=\(\displaystyle \frac{5}{3}\)cm
先に(2)が求まりましたね。

はい、正解です。

あとは(1)三角形ACDの面積ですね・・・
えっと・・・
あれ、すぐにはわからないです。

そうですね。
この後は、補助線を引かないと解けませんからね。
例えば、DからECに垂線を引いて解くことができます。
あるいは、CからEAに垂線を引いて解くことができます。
どちらの補助線でも「3:4:5の直角三角形」と「直角をはさむ辺の比が1:2の直角三角形」がつくれるので、組み合わせて解くことができます。

これらの補助線を引く解法は、知識を使わない正攻法の解法と同一なので、下で見ていくことにしましょう。
別解

さて、「3:4:5の直角三角形」の知識をまったくなしで解くならばどうなるか。
順に説明してきます。
まず、CからEAに垂線CFを引きます。
直角三角形DACを相似な三角形に割る有名な図形配置です。
直角三角形CAFも直角三角形DCFも「直角をはさむ辺の比が1:2の直角三角形」です。
また、三角形CAFと三角形CABは合同です。
CAで三角形CABを折り返したようなものです。
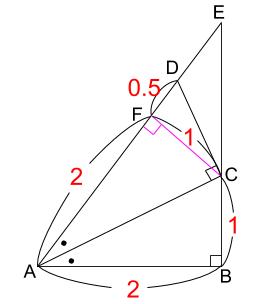

三角形ACDの面積は、
2.5×1×\(\displaystyle \frac{1}{2}\)=\(\displaystyle \frac{5}{4}\) \(cm^2\)
これで(1)が求まりました。

次に、DからEBに垂線DGを引きます。
直角三角形DCFと直角三角形DCGが合同なので、
DG=0.5、CG=1
となります。
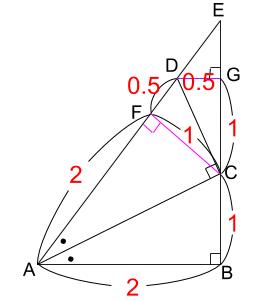

ここで、直角三角形EDGと直角三角形EABは相似です。
いわゆるピラミッド型相似ですね。
相似比は、DG:AB=0.5:2=1:4
よって、EG:EB=1:4
EG=①とすれば、
GB=④-①=③
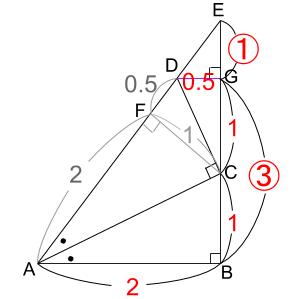

GBより、
③=2だから、
EG=①=\(\displaystyle \frac{2}{3}\)
より、CE=\(\displaystyle \frac{2}{3}\)+1=\(\displaystyle \frac{5}{3}\)
これで(2)も求まりました!
