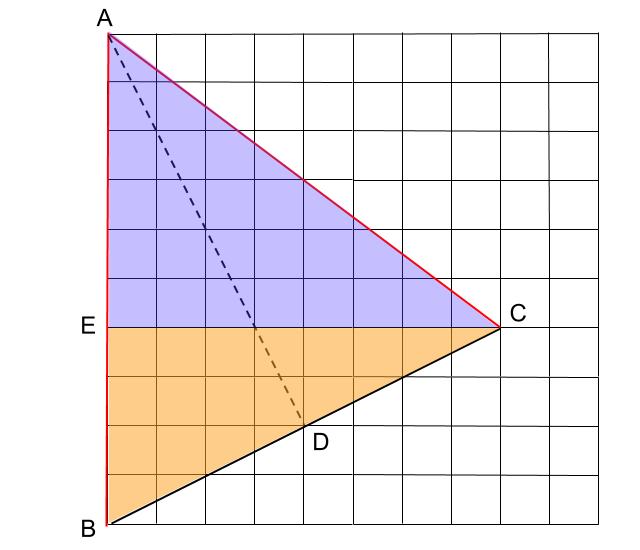
3:4:5の直角三角形
1:2と1:3の直角三角形
例題1
ABとACの長さが20cmで等しい二等辺三角形ABCがあります。
DはBCのまん中の点で、ADとBCの長さが等しいです。
また、ABとCEは垂直であり、EFとACも垂直です。
次の問いに答えなさい。
(1)EG:GCを求めなさい。
(2)EFは何cmですか。
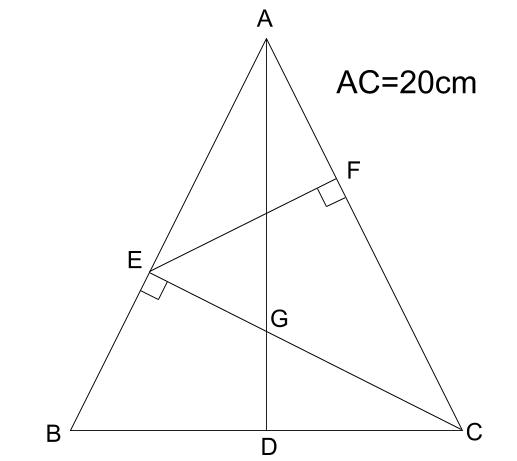
解説

ADとBCの長さが等しいので、
三角形ABDや三角形ACDが、直角をはさむ辺の比が1:2の直角三角形です。
そして、角度から三角形ABDと三角形CBEが相似とわかります。
三角形CBEも「直角をはさむ辺の比が1:2の直角三角形」ということです。
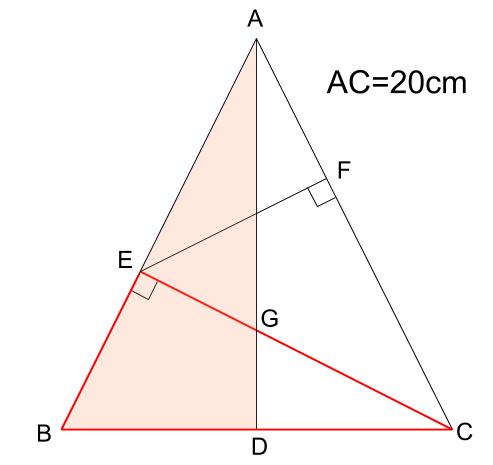

さて、「直角をはさむ辺の比が1:2の直角三角形」があるので、「3:4:5の直角三角形」が隠れている可能性があります。
絶対にそうなっているとは断定はできませんが、その可能性はあります。
この知識をもとに、「3:4:5の直角三角形」探しをしてみましょう。

三角形AEFとか、三角形ECFとか、3:4:5の直角三角形のように見えますね。
もしこの2つが3:4:5の直角三角形なら、三角形ACEだって3:4:5の直角三角形になるな。
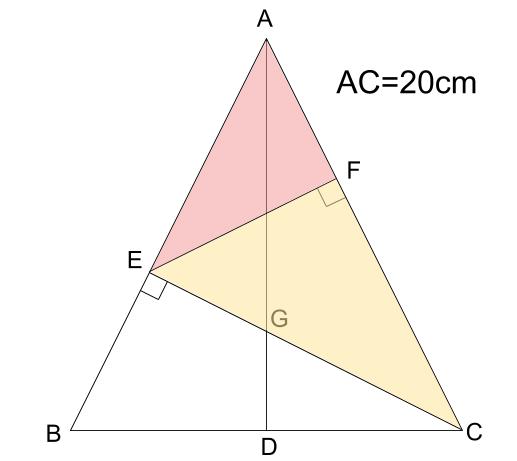

もしこれらの三角形が「3:4:5の直角三角形」ならば・・・
長さを入れてみてください。

三角形ACEのAC=20なので、
EA=12
CE=16
三角形AEFに着目すれば、EF=9.6
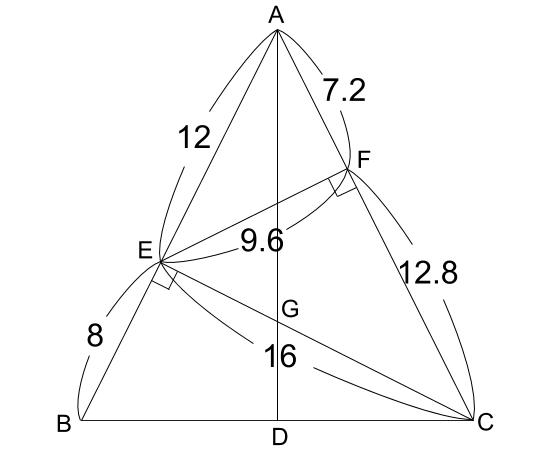

どうですか?
矛盾がないと言えますか?

えっと・・・
矛盾は今のところ見つからないですけど・・・
本当にうまくいっているのかどうかは確信が持てません。

三角形CBEに着目してみましょう。
EBが8でECが16なので、
三角形CBEが「直角をはさむ辺の比が1:2の直角三角形」になっています。
カンペキですね。うまくいっていますよ!

(2)のEFの長さが求まりましたね。
9.6cmですね。

はい、その通りです。
では(1)EG:GCを求めましょう。
続きはとても簡単だからやってみてね。

三角形AEGも直角をはさむ辺の比が1:2の直角三角形だから、
EG=6つまり、GC=16-6=10
よって、EG:GC=6:10=3:5です。

はい、とてもあっさりと解けました。
正解ですよ。
(1)EF=9.6cm
(2)EG:GC=3:5
でした。
別解

もし、「3:4:5の直角三角形があるはず!」という知識なしで正攻法で解くとどうなるか。
けっこう難しいです。
これを見ていきましょう。

まず、「直角をはさむ辺の比が1:2の直角三角形」を使うことは同様です。
EからBCに垂線をひきます。相似な直角三角形の分割として有名な図形ですね。
下図のようになります。


DはBCのまん中の点です。
ここで連比です。
あらためて、BC=⑩として書き直すと下図になります。
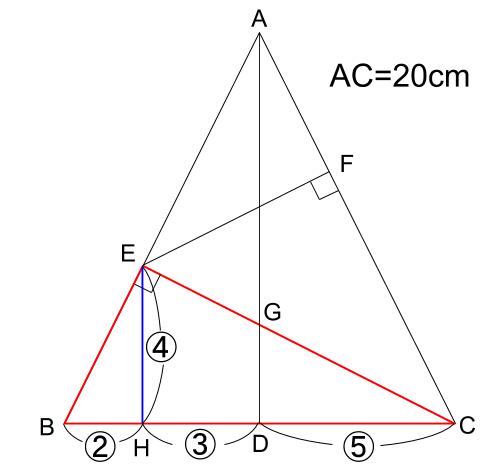

EG:GCは、三角形CGDと三角形CEHのピラミッド型相似で、3:5と求まります。

なるほど!

では続きです。
EG=3
GC=5
とします。
三角形AEGが、直角をはさむ辺の比が1:2の直角三角形なので、
AE=GC×2=6
三角形CBEが、直角をはさむ辺の比が1:2の直角三角形なので、
BE=CE÷2=4
三角形ABCは二等辺三角形なので、
AB=AC=10
下図のようになります。
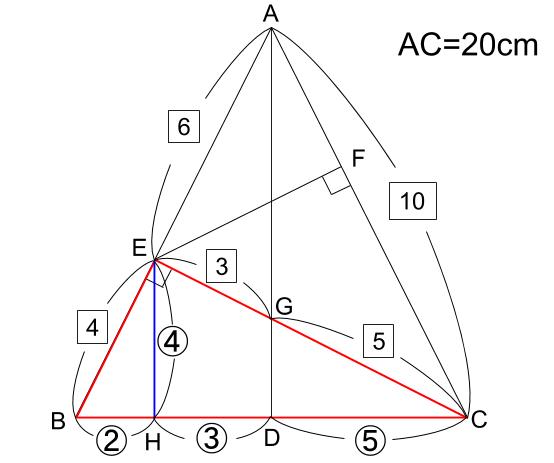

三角形AECが3:4:5の直角三角形であることが導かれました!
EFの長さは相似から求めてもよし、
面積から求めてもよし。
EF=9.6cmです。

なるほど!
うまく解けるものですね。
でも・・・裏ワザで解くのが楽ですね、えへへ。
参考図

ちなみに、三角形ABCと三角形CBEと三角形ACEの関係は、下図のようになっています。