3:4:5の直角三角形
1:2と1:3の直角三角形
例題1
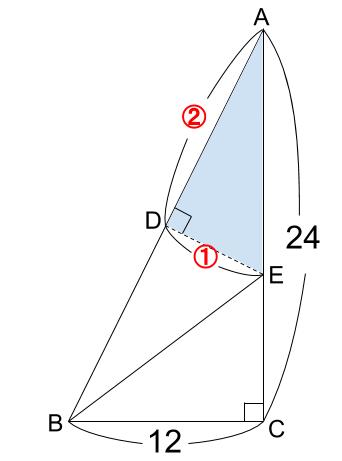
下図のように直角三角形ABCがあり、ACが24cm、BCが12cmです。
また、AがBの位置にくるように折り返すときの折れ線がDEです。
このとき、AE:ECを求めなさい。
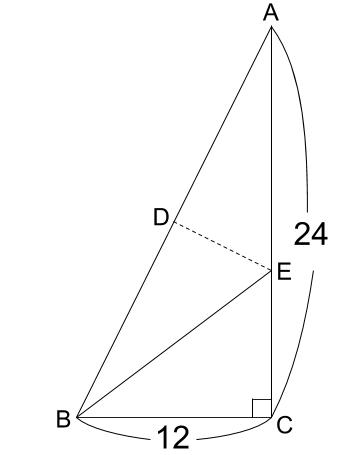
解説

直角をはさむ辺の比が1:2の直角三角形です。
このようなとき、3:4:5の直角三角形が隠れている可能性が大なのです。
これが知識です。
絶対に隠れている、とは言い切れませんが、可能性はあります。

で・・・どうすればいいの?

つまり、きちんと論理的に問題を解かなくても、答えが求まる可能性があるということです。
正攻法で解ける力をつけておくことが大事なのはもちろんですが、あっさり解ける問題を前に、わざわざ遠回りをする必要もない・・・
入試対策に限っての話ですけどね。

では見ていきましょう。
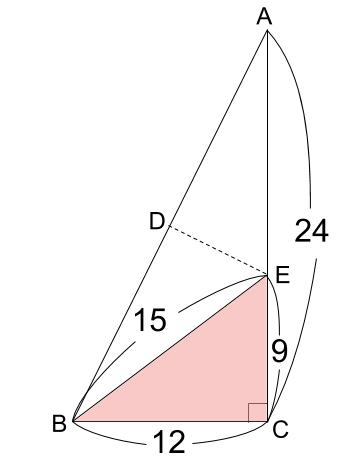
三角形EBCが、3:4:5の直角三角形のように見えませんか?
本当にそうなのか、まだわかりませんが、
もしそれが成りたつならば・・・EBとCEの長さを求めます。
BC=12なので、
EB=15
CE=9
です。
三角形EBCが、3:4:5の直角三角形なのかどうかはまだわかりませんが、
EB=15、CE=9だとすれば・・・仮定の話を進めていきます。

折り返しなので、BEとAEは等しいので、AE=15。
AE+EC=15+9=24
ACの長さは24なので、矛盾がありません。
つまり、三角形EBCが、3:4:5の直角三角形であるという予想は的中したわけです。
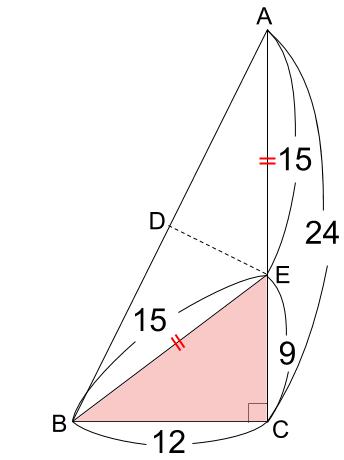

AE:EC=15:9=5:3
求まりました。
あっさり解けてしまいましたね。

え?
もう解けちゃったの?
なんだかスゴイ技ですね。

注意して欲しいことは、
どんなときにも使える技ではないということです。
自分勝手に、3:4:5の直角三角形であると決めつけて解いて、大間違いってことにならないようにしてください。
もし3:4:5の直角三角形ならば、と解いていくときは、それによって矛盾が起きないかどうか、慎重に調べつくさないといけません。

どんなときにでも使える技ではない・・・
つまり、使えるときを見きわめるのですね。

はい。
3:4:5の直角三角形がかくれていると予想すべきときは、
「直角をはさむ辺の比が1:2の直角三角形」があるとき。
「直角をはさむ辺の比が1:3の直角三角形」があるとき。
これを覚えておいてください!
別解

正攻法で解くならば以下のようになります。
スタート地点は、三角形AEDと三角形ABCが相似であると認識することです。
どちらも、「直角をはさむ辺の比が1:2の直角三角形」ですね。

で、次がちょっとハードル高いですね。
DからACに向かって垂線を引きます。
直角三角形の相似として有名な図形の分割ですから、無理というほどではないですが。
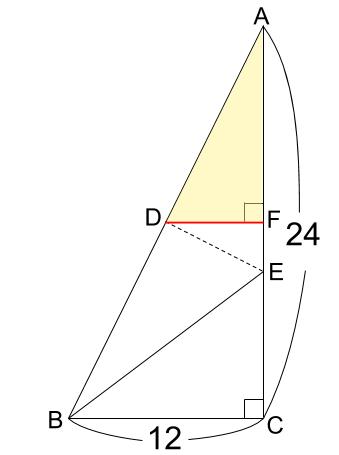

三角形ADFも三角形DEFも、直角をはさむ辺の比が1:2の直角三角形ですね。

その通りです。
直角をはさむ辺の比が1:2の直角三角形がたくさんあります。
相似ですね。
DはABの真ん中の点なので、
三角形ADFと三角形ABCは相似比が1:2
つまり、DF=6、AF=12です。
また、FEはDFの長さの半分なので、
FE=3
下図のようになります。
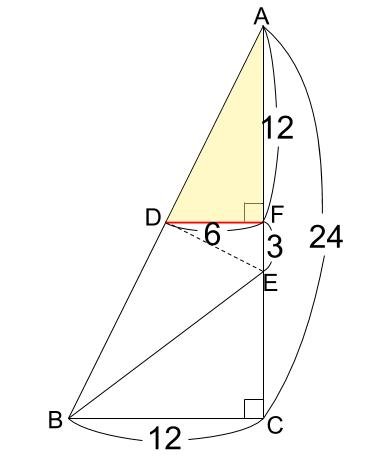

これで解決です!
AE=15と求まりました。
AE:EC=15:9=5:3

なるほどー。
この解き方だと、3:4:5の直角三角形はまったく使ってないわけですね。
参考図
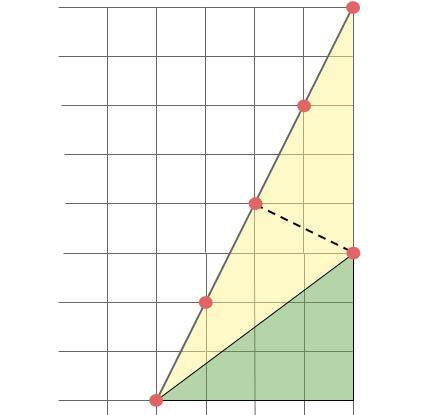

1:3でも、同じように345がでてきます。