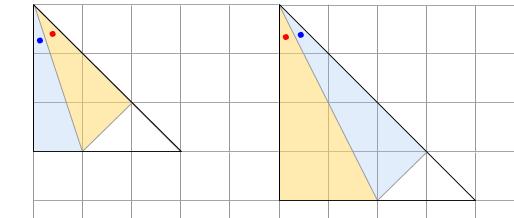
3:4:5の直角三角形
1:2と1:3の直角三角形
例題1
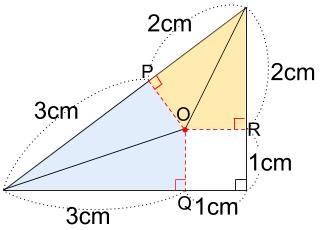
下図のように、直角三角形の内部に円があり、それぞれ点P、Q、Rで接しています。
この円の半径は何cmか求めなさい。
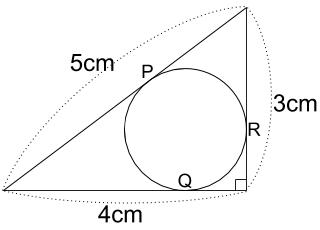
解説

円と線が接するとは、1点のみでくっついているということです。
このような円を、三角形の内接円といいます。
中学受験ではそれほど頻出ではありませんが、たまに出題されます。

よく出題されるわけではないんですね?

はい。
高校入試、つまり中学生の数学でよく見るネタです。
しかし、小学生にも理解できる話題なので、たまに出題されます。
では、まずはこの問題を学習しましょう。
円の半径が話題になっていますから、それを作図するに決まっています。
円の中心Oを目分量でいいので、自分で作図します。
その中心Oから、P,Q,Rに向かって線を引きましょう。
OP、OQ、ORが円の半径ですね。
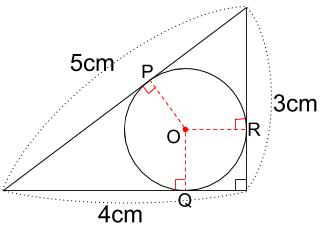

上図のように、半径と接線は垂直になります。
あたりまえの知識としてきちんと押さえておきましょう。

円の半径が何cmなのか。
これは、面積から求めることができます。
三角形の面積は、6 \(cm^2\) です。
暗算で求まりますね。
次に下図のように、3つの三角形に分けます。
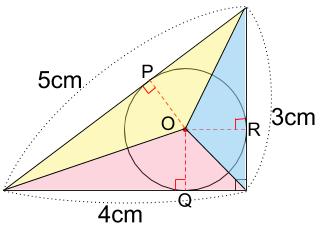

円の半径をアcmとします。
3つの三角形の高さは、すべてアcmですね。
それぞれの面積を求める式は、
青い三角形
3×ア×\(\displaystyle \frac{1}{2}\)
赤い三角形
4×ア×\(\displaystyle \frac{1}{2}\)
黄色い三角形
5×ア×\(\displaystyle \frac{1}{2}\)
これら3つの三角形の面積の和は、3つの式に共通である部分をまとめて、
(3+4+5)×ア×\(\displaystyle \frac{1}{2}\)
と求めることができます。
この値は、もちろん、はじめの三角形の面積である 6 \(cm^2\) です。
つまり、
(3+4+5)×ア×\(\displaystyle \frac{1}{2}\)=6
あとは逆算をすればアが求まります。

なるほど。
ア=1cmですね。

はい、円の半径は1cmです。
これでこの問題は解けました。
内接円の半径の長さを求めさせる問題は、中学受験ではほとんど見ません。
主に中学生以降で学ぶ内容です。
しかし、上で見たような三角形の分割とその面積については、例えばフェリス女学院などで出題されています。
知っておいて損ではありません。

さて、上で見た内接円なんですけど、ここからの話の主役は内接円ではありません。
内接円を取り除いた下の図です。

クリーム色の三角形は、
「直角をはさむ辺の比が1:2の直角三角形」
水色の三角形は、
「直角をはさむ辺の比が1:3の直角三角形」
となっています。
これこそが知っておくと有利になる知識です。
「直角をはさむ辺の比が1:2の直角三角形」や「直角をはさむ辺の比が1:3の直角三角形」があるとき、3:4:5の直角三角形が隠れていることがあるのです!
そのような問題をこれからどんどん見ていくことにしましょう。

ふーん・・・

ところで、
「直角をはさむ辺の比が1:2の直角三角形」と「直角をはさむ辺の比が1:3の直角三角形」がでてくる問題は、下の問題がとてもとても有名です。
例題1-2
下図の赤丸の角と青丸の角の大きさの和は何度か求めなさい。
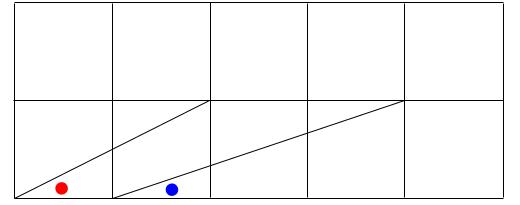
解説

角の大きさの和を求めろというのです。
赤丸の角の大きさや青丸の角の大きさは求めなくてもいいのです。
このような問題は、「和」しか求まらないことがほとんどですね。
赤丸の角だけの大きさは求まらない。
でも、赤丸の角と青丸の角の和なら求まる。
とにかく図示をしてみましょう。
赤丸と青丸の角を合わせた角は、例えば下図のようになります。
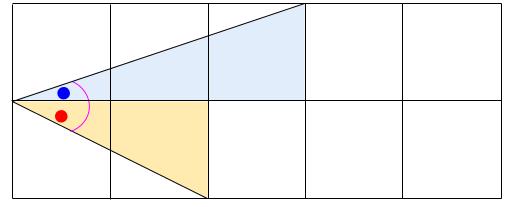

少し配置をかえると、下図のようになります。
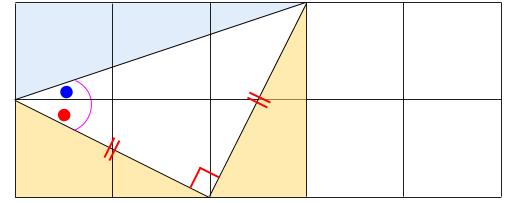

中に直角二等辺三角形ができました。
よって、45°と求まります。
こんな解法、短時間で思いつくものではありません。
まさに知識です。とにかく覚えておいてください。

はい、とにかく覚えます。

他にも、45°を説明する図形はあります。
参考程度にいくつか紹介しておきますね。
まずは、3:4:5の直角三角形との関わりの知識。
下図のように求まります。
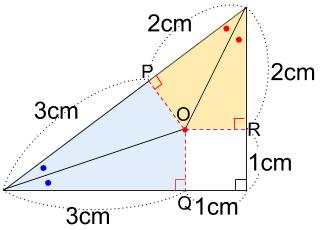

赤丸2つと青丸2つの大きさの和が90°なので、
その半分、赤丸1つと青丸1つの大きさの和は45°になります。
ちなみに、他にも下図のように45°を説明することもできます。
参考程度です。無理に覚える必要はないですよ。