水そう
棒を入れる
例題1
下図のような1辺の長さ36cmの立方体の容器に16.8cmの深さまで水を入れました。この中に、図のような直方体の棒を何本か図の向きのまま、容器の底につくまでゆっくりと入れました。

(1)棒を1本入れたときの水の深さは何cmになりますか。
(2)棒を2本入れたときの水の深さは何cmになりますか。
(3)棒を5本入れたときの水の深さは何cmになりますか。
解説

容器の底面積は、棒の底面積の何倍なのか求めます。
\(\displaystyle \frac{36×36}{12×12}\)=9
だから、
容器の底面積は⑨
棒の底面積は①
とおきます。
(1)棒を1本入れたとき
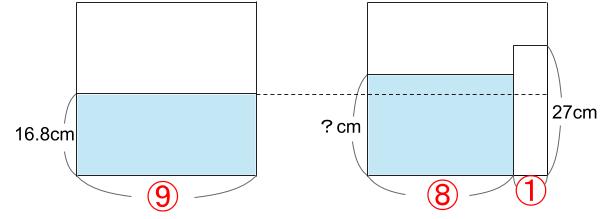

棒を入れる前と後で、水量が等しいことで解きます。
⑨×16.8=⑧×?
左右を8で割って、
⑨×2.1=①×?
〇18.9=①×?
より、?=18.9
求まりました。
18.9cmです。

正解です。
(2)棒を2本入れたとき


全く同様に水量が等しいことで解きます。
⑨×16.8=⑦×?
左右を7で割って、
⑨×2.4=①×?
〇21.6=①×?
より、?=21.6
求まりました。
21.6cmです。

正解です。
(3)棒を5本入れたとき

5本は入れすぎですね。
水位がかなり高くなるから・・・
きっと棒は水に沈むのかな?
沈まないのかな・・・
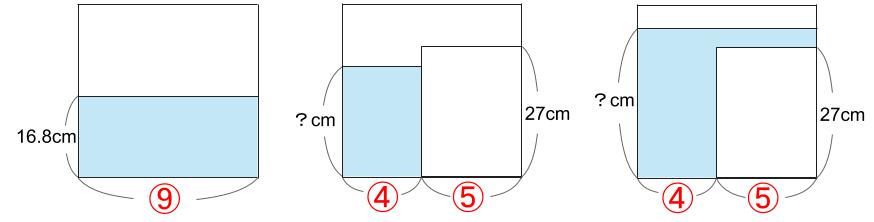

沈むのか沈まないのか、どちらであるか確定できますか?
計算してみないと分からないかな?

(1)(2)と沈まない問題でしたからね。
きっと(3)は沈むと予想します。

まあ、そういう考えも悪くはないよ。
ところで、はじめの底面積の半分の水そうに水を移すことを考えてみてください。
水の高さは、はじめの2倍になるんだけど、
これはわかりますか?

はい、わかりますよ。
底面積が②の水そうに、水が10cmまで入っていて、
底面積が①の水そうに水を移せば、深さが20cmになります。
②×10=①×20
ということです。

では、この問題では、水そうの底面積は⑨だった。
もし底面積が〇4.5の水そうに移したら?

はじめの水位は16.8cmだった。
底面積が半分になれば、水位は16.8×2=33.6cmです。

この問題、つまり棒を5本入れたとき。
底面積は④になったわけだよね。
半分の底面積〇4.5よりもせまくなったわけだ。

ということは、水位は33.6cmよりもさらに高くなる。
これは棒の高さ27cmをこえていますね!
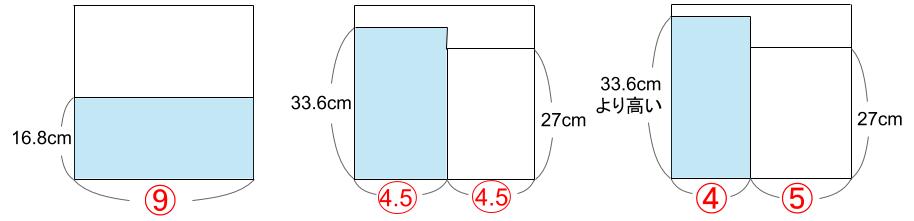

なるほど、棒は全部沈んでいることが確定します。

そうだね。
およその計算で確かめられたね。

棒は全部沈んでいることが確定している。
棒の体積の分だけ、水位がアップした!
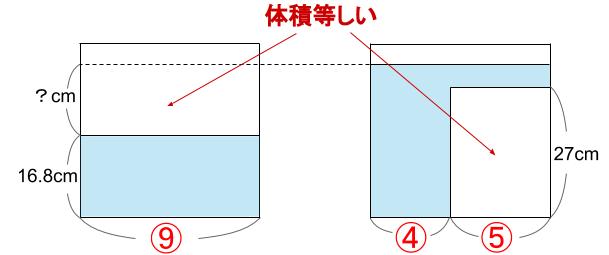

上図のように、水位のアップした分を?cmとすると、
⑨×?=⑤×27
左右を9で割って、
①×?=⑤×3
?=15
はじめの水位が16.8cmだから、
16.8+15=31.8
求まりました。
31.8cmです。

はい、正解です。
ちなみに底面積が④のときの水位は、⑨×16.8÷④=37.8cm
水そうの高さをこえています。
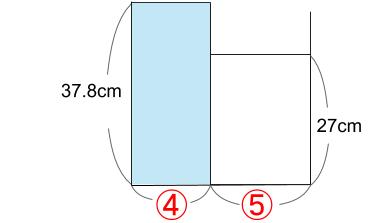

飛び出た部分を平らにならします。
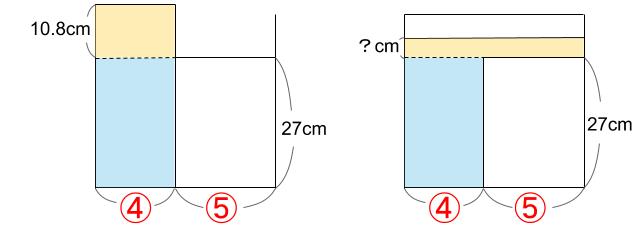

クリーム色部分を平らに均します。
④×10.8÷⑨=4.8cm
27+4.8=31.8cm
このように求めてもOKです。
