水そう
棒を入れる
例題1
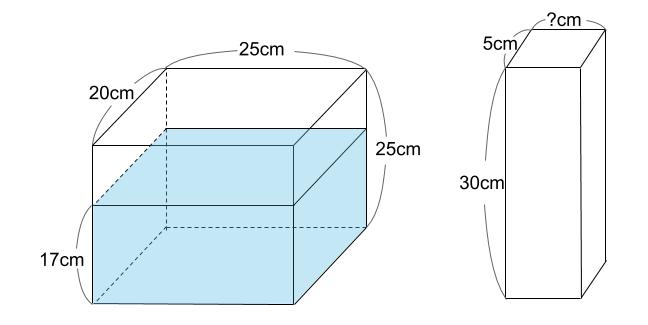
下図のような直方体の容器に、水が深さ17cmまで入っています。この容器に、図のような直方体の棒を図の向きのまま、容器の底につくまでゆっくりと入れたところ、水の深さは20cmになりました。直方体の棒は、たて5cm、高さ30cmです。直方体の棒の横の長さを求めなさい。
解説

これは以前にも解いた問題なんですよ。
今回は「底面積の比」を使って解くとどうなるか、
これがテーマになります。
さっそく見ていきましょう。

棒を入れる前も、入れた後も、
(水量)=(底面積×高さ)
ですね。
つまり、
(棒を入れる前の底面積×前の高さ)=(棒を入れた後の底面積×後の高さ)
となります。
ここで比が大活躍します。
下図のようになります。
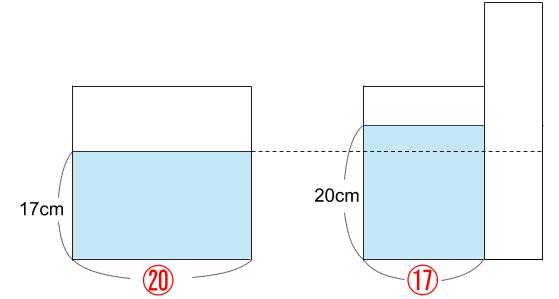

底面積が、上図のように
⑳と⑰と表せます。
(棒を入れる前の底面積×前の高さ)=(棒を入れた後の底面積×後の高さ)
⑳×17=⑰×20
ということです。
2つの「かけ算」が等しくなるためには、
互に逆の数をかけ合わせることになります。
九九でもそうでしたね。
例えば、三六(さぶろく)と六三(ろくさん)が等しいようにです。

なるほど。
ということは、棒の底面積は、⑳-⑰=③ですね。
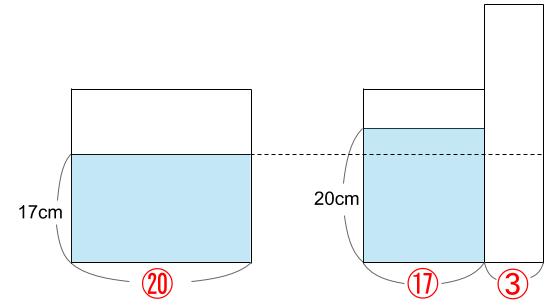

容器の底面積に着目して、
⑳=20×25 \(cm^2\) だから、
左右を20で割れば、
①=25
棒の底面積③は、
③=75
つまり、5×?=75
なので、
?=15
あっさりと解けてしまいました!
すごいかも・・・

はい、正解です。
