水そう
棒を入れる
例題1
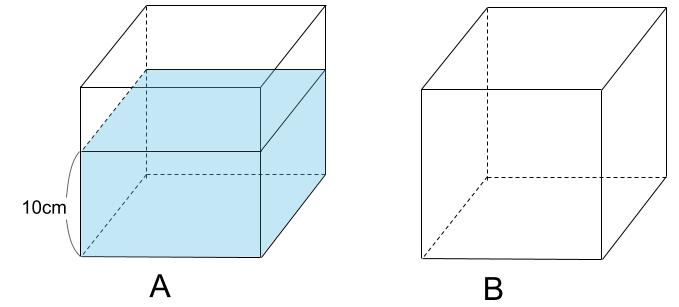
下図のような直方体の水そうAとBがあります。
AとBは、まったく同じ大きさの水そうです。
水そうAに水を深さが10cmになるように入れました。
この水の一部を、水そうAから水そうBに移し、
2つの水そうの水位が同じになるようにしました。
このとき、水位は何cmですか。
解説

水が半分ずつにわけられたのだから、
10÷2=5
5cmですね。

はい、正解です。

ここで学んで欲しいことは、「具体値がなくてもわかることがある」
ということです。
水量や底面積がいくつなのか、まったくわからない問題でしたが、
水位5cmは求められたわけですね。
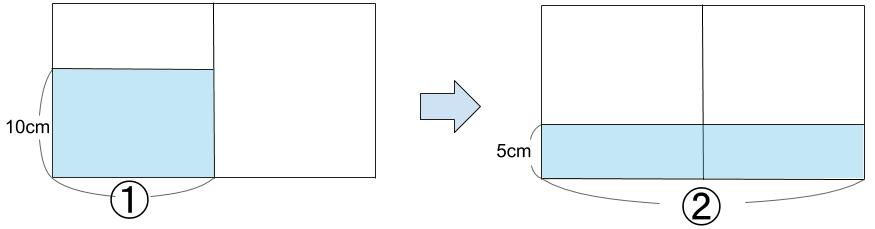
水そう1つの底面積が①ならば、
水そう2つの底面積は②。
水量は、
①×10=⑩
②×5=⑩
等しい水量です。
例題2
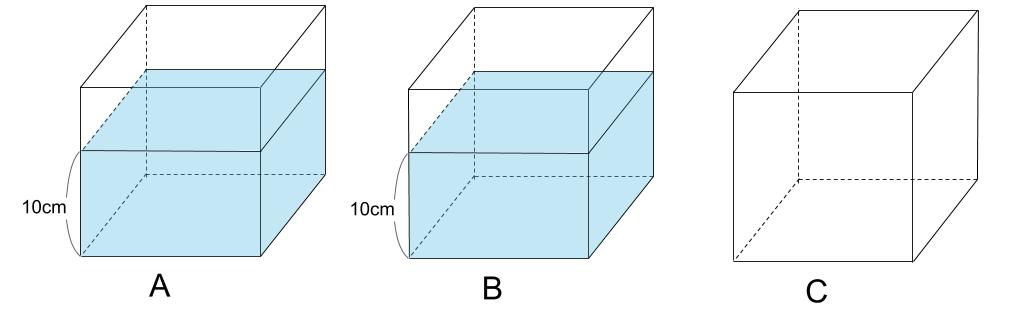
下図のような直方体の水そうA、B、Cがあります。AとBとCは、まったく同じ大きさの水そうです。
水そうAと水そうBに水を10cmの深さになるまで入れます。
この水を、3つの水そうの水位が同じになるように移しました。
このとき、水位は何cmになりましたか。
解説

これも具体値がない問題ですね・・・
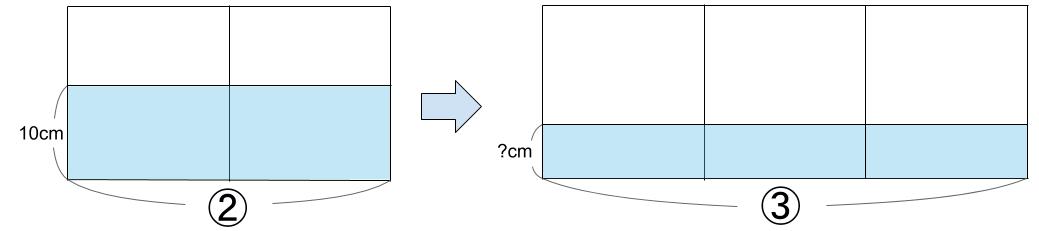

水量の合計が、2通りで表せます。
(底面積2つ分)×10cm=(底面積3つ分)×?cm
ということです。
つまり、
②×10=③×?
?は計算するだけです。

?=\(\displaystyle \frac{20}{3}\) cm
つまり、6\(\displaystyle \frac{2}{3}\) cmです。

正解です。
このように、具体的な値ではなくて、②や③のような値で計算処理をすることができます。
これは、「底面積の比」を利用している解き方です。
もし「比」をまだ習っていなかったとしても大丈夫です。
きっちり分かりやすく教えていきます。
「底面積の比」を利用することを身につけましょう。
計算が簡単になりますし、解き方も簡単になることが多いです。
