水そう
棒を入れる
例題1
下図のような底面積が1000 \(cm^2\) で高さが50cmの直方体の容器に水を入れ、たて10cm、横20cm、高さが50cmの直方体の棒を図の向きのまま、容器の底につくまで入れました。その後、直方体の棒を底から6cm引き上げると水の深さは何cm低くなりますか。
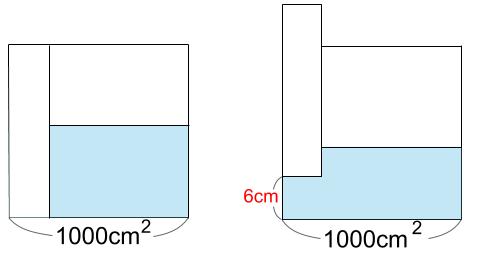
解説

この問題では、
容器の底面積が1000\(cm^2\)
棒の底面積が、10×20=200\(cm^2\)
\(\displaystyle \frac{1000}{200}\)=5倍なので、
容器の底面積が⑤
棒の底面積が①
とおけますね。

「底面積の比」を利用した場合、
ほとんどの問題が水量が等しいことを式にして、
「棒を入れる前の底面積×前の高さ」=「棒を入れた後の底面積×後の高さ」
この等式1つで解けてしまいました。
とても簡単にワンパターンで解けることを今までは見てきたのです。

はい、そうですね。
でも今回は、
「前の底面積×前の高さ」=「後の底面積×後の高さ」
では解けそうもありませんね。

そうなんです。
こんなときは別の視点で解くのです。
「底面積の比」を利用する前に練習した視点です。

えっと・・・確か・・・
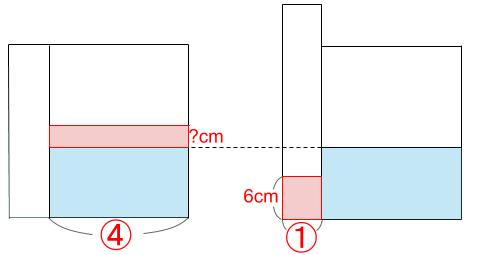
棒を入れて邪魔した分だけ、そこにあった水が上に行く。

その通りですね。
下図のピンクの水量が等しいのです。

なるほど・・・
④×?=①×6
?=1.5cmだ。
1.5cm低くなります。

はい、正解です。
別解

上の解法でおしまいで良いのだけど、
一応別解も紹介しておきます。
この問題も、
「前の底面積×前の高さ」=「後の底面積×後の高さ」
で解くことができるのです。
下図の紫色の部分。高さは不明ですが、これをacmとしておきます。
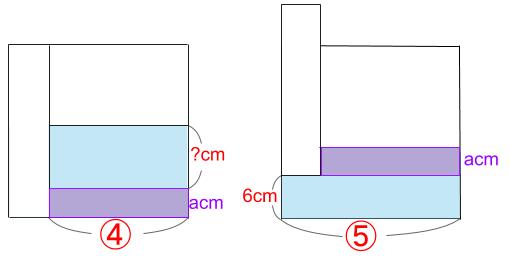

残りの水量は等しいので、
④×?=⑤×6
?=7.5cm

なるほど・・・
はじめは、a+7.5cm
棒を抜いたら、a+6cm
1.5cm低くなった。
求まりましたね。

普通はこの別解でなくて、はじめの解き方で解くんじゃないかな。
まあ参考程度に紹介しました。
