水そう
棒を何本も入れる
例題1
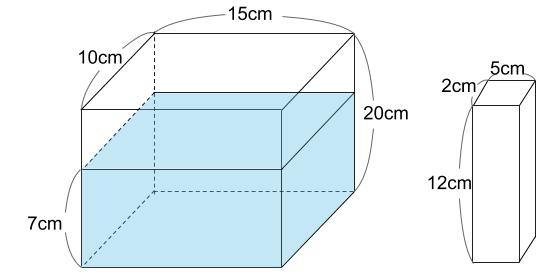
下図のような直方体の容器に、7cmの深さまで水を入れました。この中に、図のような直方体の棒を何本か図の向きのまま、容器の底につくまでゆっくりと入れました。
(1)棒を1本入れたときの水の深さは何cmになりますか。
(2)棒を3本入れたときの水の深さは何cmになりますか。
(3)棒を7本入れたときの水の深さは何cmになりますか。
解説
(1)1本
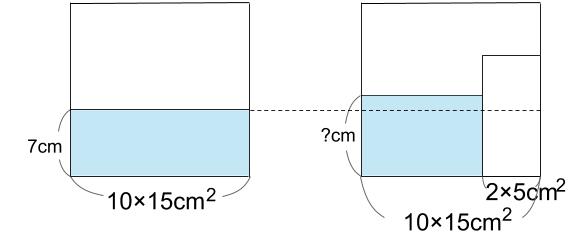

容器の底面積は、10×15=150 \(cm^2\)
棒1本の底面積は、2×5=10 \(cm^2\)
棒を入れる前と後で、水量が等しいことを式にします。
150×7=140×□
□=7.5cm
簡単ですね!
7.5cmです。

正解です。
(2) 3本
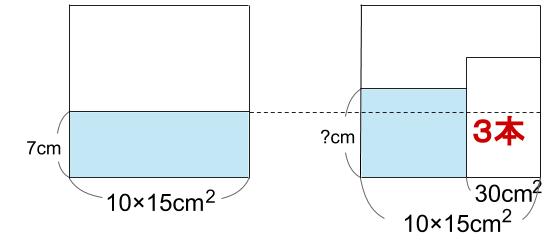

棒を3本入れると、底面積は30 \(cm^2\) 減りますね。
150-30=120
棒を入れる前と後で、水量が等しいことを式にします。
150×7=120×□
等式の左右を30で割って、
5×7=4×□
等式の左右を4で割って、
\(\displaystyle \frac{5×7}{4}\)=□
□=\(\displaystyle \frac{35}{4}\)cm
簡単ですね!
\(\displaystyle \frac{35}{4}\)=8\(\displaystyle \frac{3}{4}\)=8.75cmです。

正解です。
(3)7本

さすがにワンパターンですね・・・
つまり、ワナがある・・・
棒を7本入れると、底面積は70 \(cm^2\) 減ります。
150-70=80
棒を入れる前と後で、水量が等しいことを式にします。
150×7=80×□
□=\(\displaystyle \frac{105}{8}\)=13\(\displaystyle \frac{1}{8}\)
つまり、13.125cm
これが答えじゃない可能性がありますね。
図にしてみると・・・
棒の高さ12cmだから、おかしいですね。
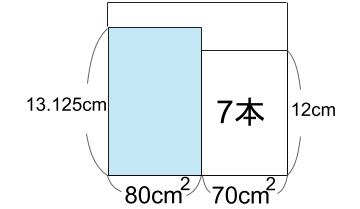

よく気がつきました!すばらしいです。
上に飛び出た部分の水が、おかしいよね。
実際はどうなるかを図示します。
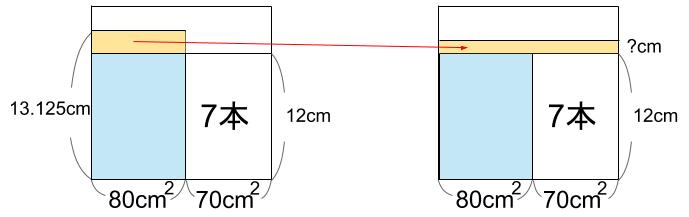

上に飛び出た部分の水を、平らに均します!
左のクリーム色部分と右のクリーム色部分は体積が等しいことから解けますね。

80×(13.125-12)=150×?
1.125=\(\displaystyle \frac{9}{8}\) だから、
80×\(\displaystyle \frac{9}{8}\) =150×?
90=150×?
左右を30で割って、
3=5×?
つまり、?=0.6
より、水位は、12+0.6=12.6cmです。

正解です。
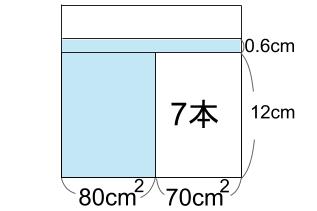

全部しずむことが分かったあとの水位の求め方は、
「棒7本の体積」=「水位の上がった分」
でも解けます。
上がった水位を?cmとすると、
70×12=150×?
より、?=\(\displaystyle \frac{70×12}{150}\)=\(\displaystyle \frac{28}{5}\)=5.6
はじめの水位7cmから5.6cm上がれば、12.6cm
このように求めてもOKです。
