水そう
おもりを重ねて入れる
例題1
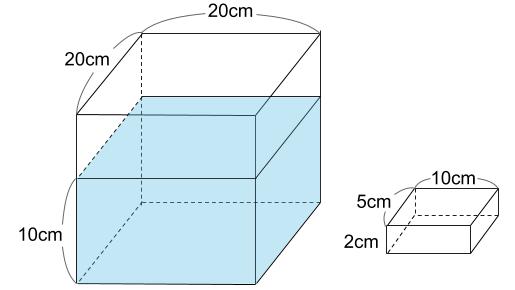
下図のような直方体の容器に、水が10cmの深さまで入っています。この中に、図のような直方体の重りを図の向きのまま、1個ずつ重ねて沈めていきます。
(1)重りを1個沈めたときの水の深さは何cmになりますか。
(2)重りを2個重ねて沈めたときの水の深さは何cmになりますか。
(3)重りを6個重ねて沈めたときの水の深さは何cmになりますか。
解説
(1)1個
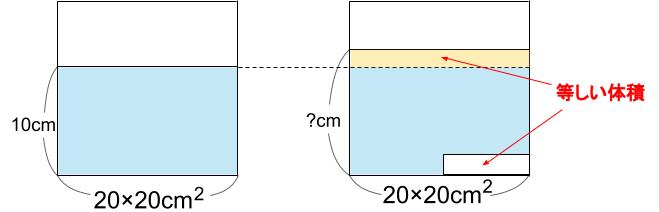

おもりの体積と、上がった水の体積が等しい。
高くなった水位を□cmとすると、
10×5×2=20×20×□
左右を100で割ると、
1=4×□
つまり、□=\(\displaystyle \frac{1}{4}\)
\(\displaystyle \frac{1}{4}\)cm 水位が上がったのだから、10+\(\displaystyle \frac{1}{4}\)=10\(\displaystyle \frac{1}{4}\)
求まりました、10.25cmです。

はい、正解です。
もちろん分数で答えてもOKです。
(2)2個
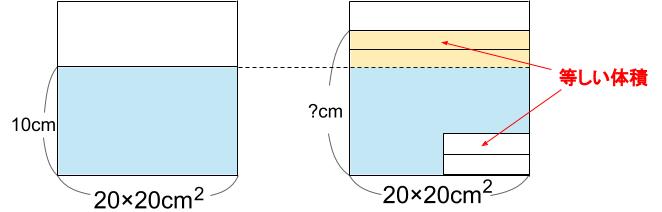

おもり1つで水位が0.25cmアップしました。
おもり2つなら、0.25×2=0.5cmアップしますね。
10+0.5=10.5
水位は、10.5cmです。

はい、正解です。
(3)6個

おもり1つで、水位が0.25cmアップしました。
おもり6つなら、0.25×6=1.5
1.5cmアップする。
つまり、10+1.=11.5cm
こんな簡単でいいのかな・・・
何かひっかけがある?

ひっかけるつもりなんてないのだけどね。
11.5cmでは間違いです。
正しい答えを求めましょう。

えっと。何が間違いなんだろうか・・・

ちゃんと図をかかないからですよ。
6個のときの図は?

下図のようになります。
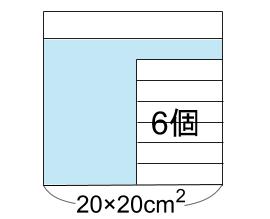

本当にそうなるのかな?
他の可能性もあるはずだよ。

え?

だって、おもりが全部沈む保証はないよね。

あ・・・え?
あ、そうか。

おもりが全部沈むならば、1.5cmアップで正解です。
図には情報をちゃんといれないといけない。
おもり6個の高さは、2×6=12cm
おかしいじゃないですか!
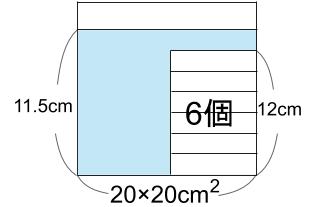

確かに・・・
水位とおもりの高さがおかしいです。

これはね、おもりは全部しずまないということなんだよ。
つまり下図のようになるんだ。
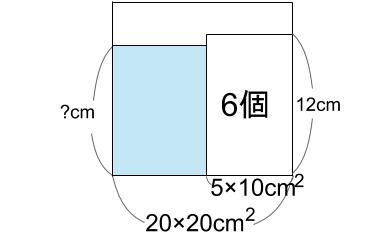

水ははじめ
20×20×10=4000 \(cm^3\)
おもりを入れたあとの水の底面積は、400-5×10=350 \(cm^2\)
つまり、
4000=350×?
左右を50で割って、
80=7×?
つまり、?=\(\displaystyle \frac{80}{7}\)=11\(\displaystyle \frac{3}{7}\)
求まりました。水位は、11\(\displaystyle \frac{3}{7}\) cmです。
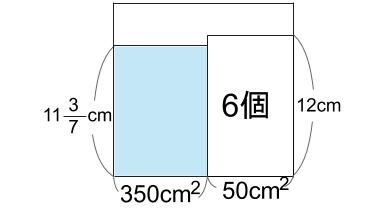

水位とおもりの高さが、うまくいってます。これは自信があります!

はい、正解です。
このように、おもりが全部しずむのか、しずまないのか。
この点にも注意しないといけない問題があるのです。
覚えておきましょうね。

おもりが全部しずむのか、しずまないのか。
見分け方はあるんですか?

それはね、計算してみないとわからないんだ。
つまり、
「全部沈むならば」という仮定で水位を求めて、矛盾が起きるかどうかを判定します。
矛盾がないならば、その値が正しい水位です。
矛盾があれば、全部沈まないのが正しいので、計算をやり直します。
矛盾がないとは、
求めた水位が、おもりの高さより高いときです。
全部沈むという仮定と一致しているということです。

あるいは、
「全部沈まないならば」という仮定で水位を求めます。
矛盾がないならば、その値が正しい水位です。
矛盾があれば、全部沈むのが正しいので、計算をやり直します。
矛盾がないとは、
求めた水位が、おもりの高さより低いときです。
全部沈まないという仮定と一致しているということです。
