水そう
棒を入れる
例題1
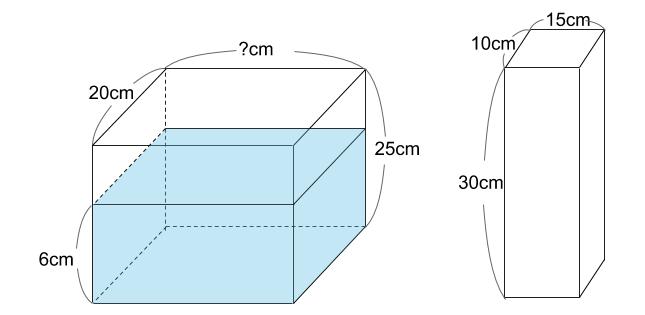
下図のような直方体の容器に、水が深さ6cmまで入っています。この容器に、図のような直方体の棒を図の向きのまま、容器の底につくまでゆっくりと入れたところ、水の深さは9.6cmになりました。容器は、たて20cm、高さ25cmです。容器の横の長さを求めなさい。
解説

まずは図示ですよ。
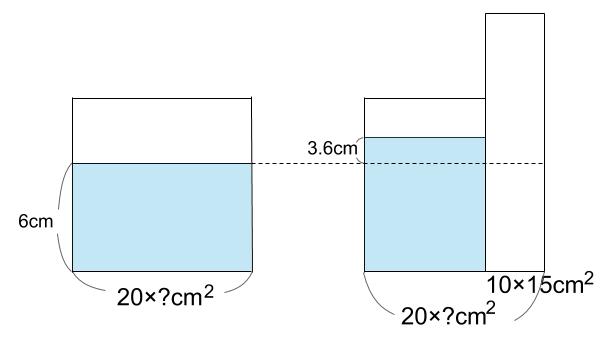

さて、3通りの解き方がありましたね。
どれで解いたら楽に解けそうなのか、わかります?

やってみないとわからないですよ。

はい、そうですね。
どれで解くと楽なのかは、やってみないとわからないでOKです。
初学者は、3つの解き方をすべて試してみるというスタンスで学習していきましょう!
解き方Aタイプ:水量は変化しない(底面積×高さ)
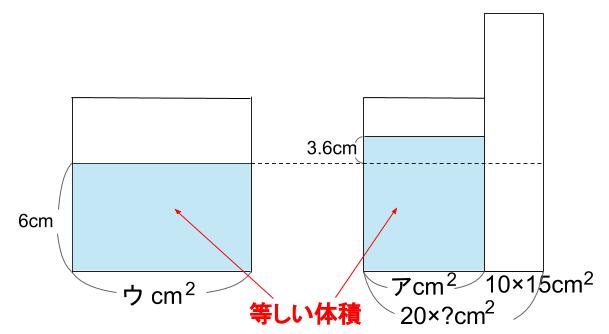

水そうの底面積をウ \(cm^2\) 、
右の水部分の底面積をア \(cm^2\) とします。
ウ×6=ア×9.6
えっと・・・続きは・・・

ここから先は、計算テクニックになります。
かけ算が等しいときは、互いに逆の数をかける。
ウ=〇96、ア=〇60とすれば、
〇96×6=〇60×9.6
これでうまくいきます。
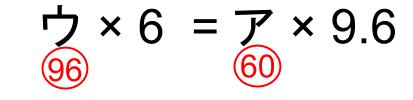

はい、わかりました。
〇96×6=〇60×9.6
左右を12で割ると、
⑧×6=⑤×9.6
水そうの底面積をウ \(cm^2\) が⑧
右の水部分の底面積をア \(cm^2\) が⑤
とおけるので、下図のようになります。
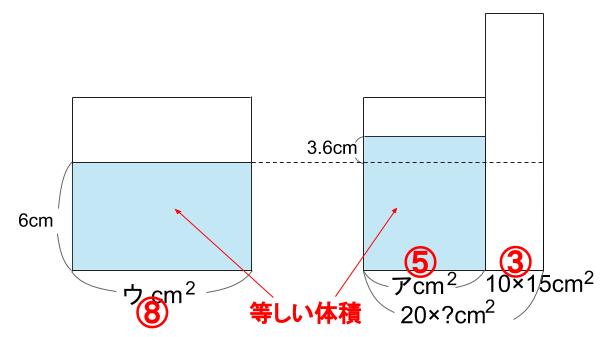

棒の底面積は、⑧-⑤=③
ということか。
③=10×15
なのだから、
①=50
水そうの底面積は、⑧=400
つまり、20×?=400
だから、?=20
求まりました。20cmです。

はい、正解です。
解き方Bタイプ:棒が押しのけた水=上がった水
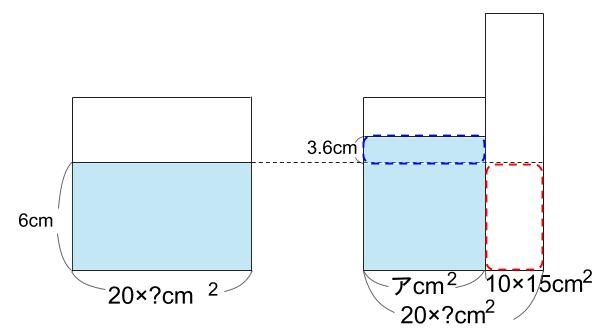

棒を入れたときの水部分の底面積をア \(cm^2\) とすると、
ア×3.6=10×15×6
左右を0.6でわると、
ア×6=10×15×10
左右を6でわると、
ア=250
より、水そうの面積は、250+150=400 \(cm^2\)
つまり、20×?=400
だから、?=20
求まりました。20cmです。

はい、正解です。
解き方Cタイプ:Bタイプの変形
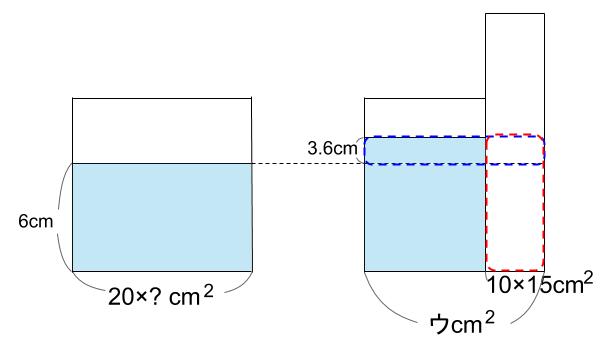

水そうの底面積をウ \(cm^2\) とすると、
ウ×3.6=10×15×9.6
0.6で割って
ウ×6=10×15×16
3で割って
ウ×2=10×5×16
2で割って
ウ×1=10×5×8
ウ=10×5×8=400
つまり、20×?=400
だから、?=20
求まりました。20cmです。

はい、正解です。
