水そう
棒を入れる
例題1
下図のような直方体の容器に、水が深さ17cmまで入っています。この容器に、図のような直方体の棒を図の向きのまま、容器の底につくまでゆっくりと入れたところ、水の深さは20cmになりました。直方体の棒は、たて5cm、高さ30cmです。直方体の棒の横の長さを求めなさい。
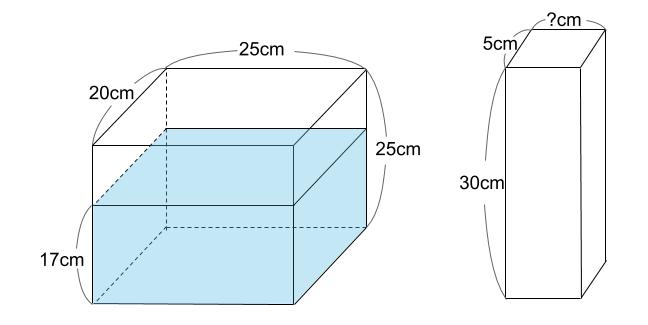
解説

まずは図示ですよ。
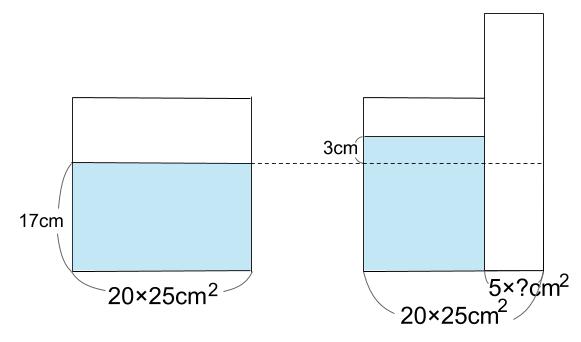

さて、3通りの解き方がありました。
どれで解いたら楽に解けそうなのか、わかります?

やってみないとわからないですよ。

うん、そうなんだよ。
どれで解くと楽なのかは、やってみないとわからないでOKです。
3つの解き方、すべて試してみるというスタンスが、初学者には絶対におすすめなんです。
では、先ほどと同じ順番で解いていってみようか。
解き方Aタイプ:水量は変化しない(底面積×高さ)
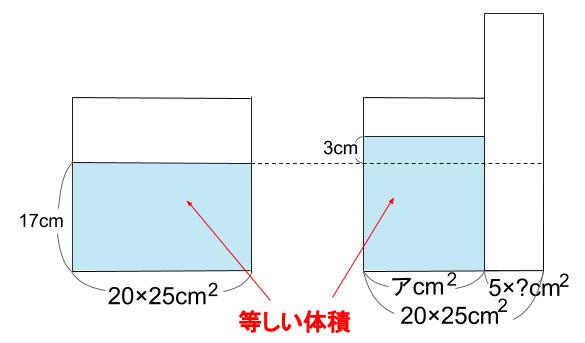

右の水部分の底面積をア \(cm^2\) とします。
20×25×17=ア×20
左右を20で割って、
25×17=ア
アは計算するだけですね。
ア=25×17=425
つまり、棒の底面積は、20×25ー425=75 \(cm^2\)
5×?=75
なので、?=15
求まりました。

正解です。
解き方Bタイプ:棒が押しのけた水=上がった水
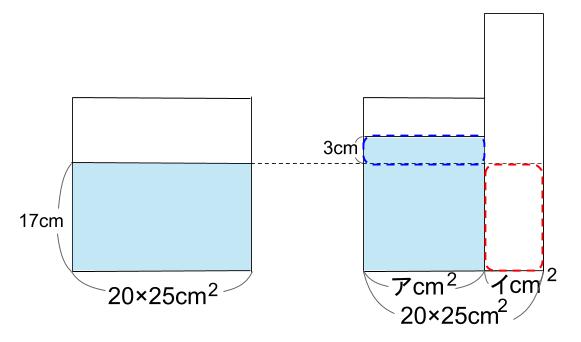

右の水部分の底面積をア \(cm^2\) とします。、
棒の底面積をイ \(cm^2\) とします。
赤い点線部分と青い点線部分は等しいことを式にします。
ア×3=イ×17
えっとこれは・・・

これは比の処理になります。
比を習ってない人も、読めばわかるように説明していくので、できれば身につけてしまいましょう。
ア×3=イ×17
のようにかけ算が等しいとき、逆の数をかけます。
ア=⑰
イ=③ということです。
⑰×3=③×17
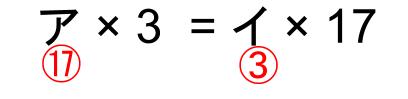

右の水部分の底面積がア \(cm^2\) で、⑰
棒の底面積がイ \(cm^2\) で、③
つまり、水そうの底面積が、⑰+③=⑳
下図のようになります。


水そうの底面積より、20×25=⑳
より、①=25
③=75なので、
棒の底面積は75 \(cm^2\) です。
5×?=75
なので、?=15
求まりました。

正解です。
解き方Cタイプ:Bタイプの変形
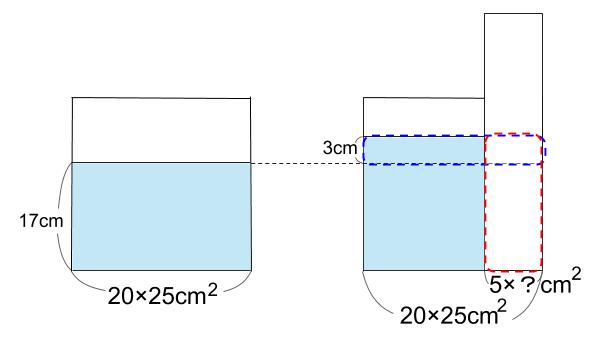

5×?×20=20×25×3
左右を20で割って、
5×?=25×3
左右を5で割って、
?=5×3
より、?=15
これが一番計算が楽でしたね。

そうだね。
結局「棒の底面積」を知りたかったわけだ。
しかし、前の2つは、
「水そうの底面積-棒の底面積」という値が必要だった。
3つめの解き方だけ、「棒の底面積」そのもので式を作れたからなんだよ。
