水そう
棒を入れる
例題1
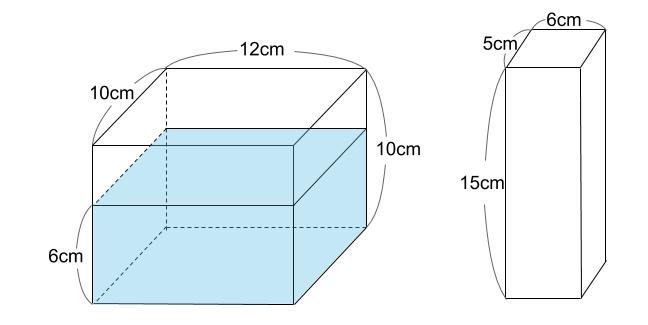
下図のような直方体の容器に、水が深さ6cmまで入っています。この容器に、図のような直方体の棒を図の向きのまま、容器の底につくまでゆっくりと入れます。
水の深さは何cmになりますか。
解説

この問題も、水そうを前面から見た図で解きましょう。
こんな図になりますね。
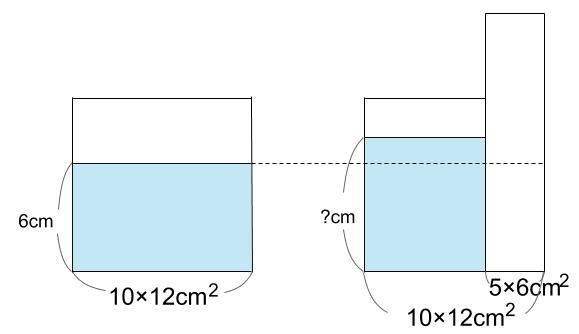

解き方は3種類あります。
順番に説明します。
解き方Aタイプ:水量は変化しない(底面積×高さ)

水は棒を入れる前と後で同じ量ですね。
つまり、棒を入れる前と後で、2つの水の量が等しいという解き方です。
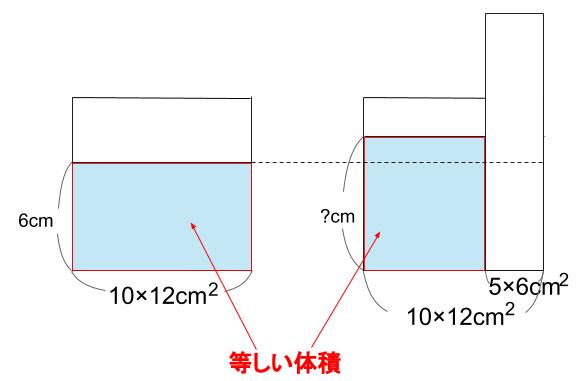

水の体積は棒を入れる前と後、どちらも
「底面積×高さ=水の体積」
で求められます。
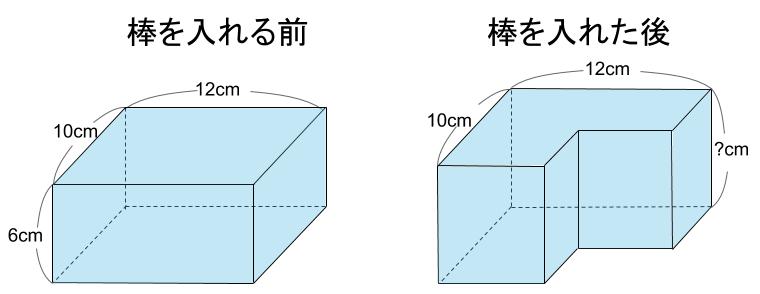
水の形は、
棒を入れる前は四角柱(直方体)
棒を入れた後は、六角柱です。
どちらも柱体で、その体積は、「底面積×高さ」で求められます。

棒を入れる前は、10×12×6\(cm^3\)
棒を入れた後は、(10×12-6×5)×?\(cm^3\)
これらが等しいから、等式にするんですよね。
10×12×6=(10×12-6×5)×?

はい。
とてもいいですね。
今回は計算が楽な数値ですね。
10×12×6=(10×12-6×5)×?
右側の()の中を計算して、
10×12×6=90×?
左も右も10で割って、
1×12×6=9×?
左も右も9で割って、
?=8と求まります。
解き方Bタイプ:棒が押しのけた水=上がった水

解き方は他にもあります。
下図の点線で囲まれた部分の体積が等しくなります。
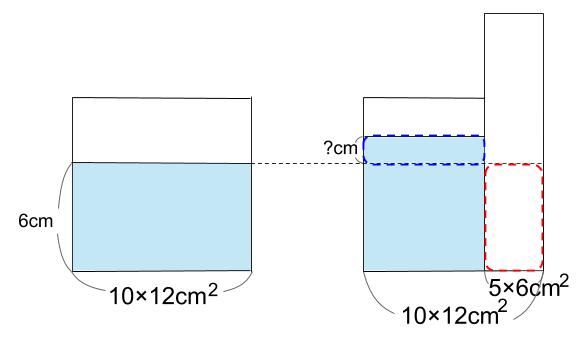

赤い点線部分には、棒を入れる前に水がありました。
ここに棒が入ったために、水は他に移動することとなった。
その移動先が、青い点線部分になります。

なるほど!
赤い点線部分の体積は、5×6×6\(cm^3\)
青い点線部分の体積は、(10×12-5×6)×?\(cm^3\)
これらが等しいから、
5×6×6=(10×12-5×6)×?

はい、その通りです。
続きの計算をしてみてね。

5×6×6=(10×12-5×6)×?
()の中を計算して、
5×6×6=90×?
左も右も6で割って、
5×6×1=15×?
もうわかります。
?=2
です。

はい、その通りです。
今回は、上がった水位を?としていたから、はじめの水位6cmと足して、
6+2=8
8cmと求まりますね。
解き方Cタイプ:Bタイプの変形

さらに、もう1つの解き方です。
先ほどの着眼点に、さらに下のクリーム色部分も加えます。
青い点線部分と赤い点線部分が等しいのなら、
どちらにもクリーム色部分を加えたものも等しい。
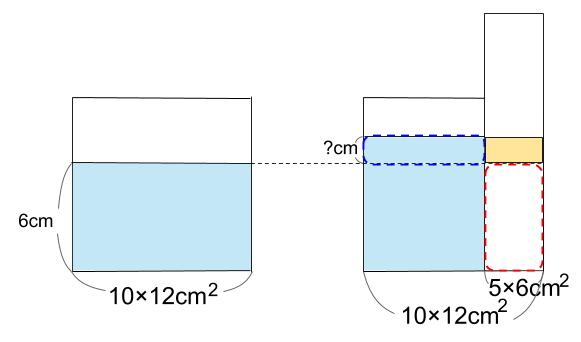

つまり、下図の点線で囲まれた部分の体積が等しいということです。
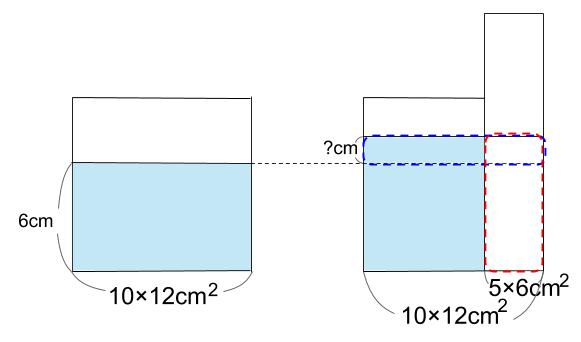

なるほど!
赤い点線部分の体積は、5×6×(6+?)\(cm^3\)
青い点線部分の体積は、10×12×?\(cm^3\)
これらが等しいから、
5×6×(6+?)=10×12×?
では、等式を簡略化してきます。
左右を30で割って、
(6+?)=4×?
あれ・・・これはどうやって求めればいいですか?

左右どちらにも「?」があって、ここで困ってしまうよね。
ここから先は、新しい計算技術に慣れていってもらうしかない。
「?」がいくつなのかはわからないけど、「4倍」は線分図では表現できるよね。
「?」を4倍したものと、「?+6」が等しいので下図のようになります。
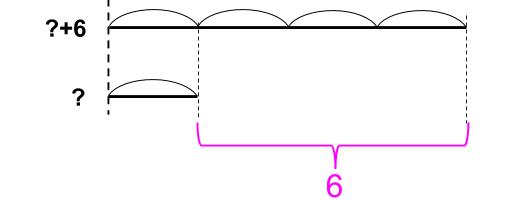

なるほど!
3山分が6だから・・・
1山分が2
?=2
?+6=8
ちゃんと4倍になっている!
?=2cmと求まります。

同じように、線分図で「~倍」を学習したことがあったよね。
4年生のころかな。
山を何個もかくのではなくて、
4山を④
1山を①
と表すのが便利だったよね。
つまり、「?=①」とおいて、
①+6=①×4
ということです。
つまり、
①+6=④
この式から、6=③がわかるので、
3で割って、①=2と求まります
この〇数値を使った計算方法はとてもとても便利です。
必ずマスターしましょう!
これは比を使っているのと同じことです。
比をすでに習っている人は、どんどん使っていきましょう。
比を習っていなくても、恐れることはありません。
解説のように解く練習をしていきましょう!

でも・・・この解き方Cは難しいですね・・・
解き方Aとか解き方Bで解いた方が簡単ですよね?

解き方Cでは解きにくかったですね。
今回は、最後の水位が不明で、これを求める問題でした。
でもね、最後の水位は15cmでした、水そうの底面積を求めなさい。
とか、どこを与えてどこを隠すかで問題が変わります。
そのさい、上の3パターンの解き方のうち、どれを選べば簡単なのかは、そのときによって違いますからね。

えーーーそうなの・・・

計算技術に長けれていれば、1つの解法だけですべての問題が解けます。
A、B、Cどの1つでもです。
でもね、3パターンの解き方を覚えた方が簡単ですよ。
はじめのうちは、3パターンの解き方のどれも試してみることをおススメします。
そのうち、自分なりに、こういうときはこう解くっていうスタイルができてくるかもしれない。それまでは3パターンの解き方をすべて練習しておきましょう!!
