水そう
棒を入れる
例題1
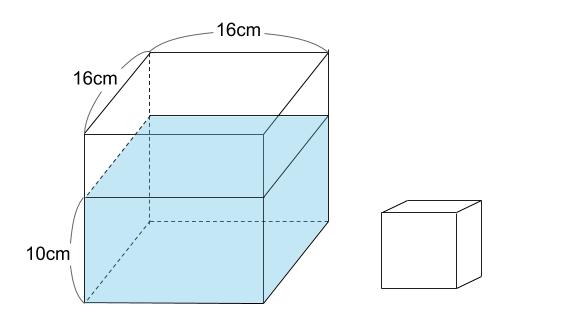
下図のような、1辺の長さが16cmの立方体の水そうに、水が深さ10cmまで
入っています。この水そうに、1辺の長さが8cmの立方体のおもり入れます。
水の深さは何cmになりますか。
解説

おもりを水そうに入れると、水位が上がるのはわかるよね。

水に浮かないおもりを入れるんですよね。
もちろん、水位が上がりますよ。
お風呂に入ったときみたいに。

そうだね。水の深さが深くなるよね。
このような問題は、必ず図示をして解きましょう。
より複雑な問題に出会ったとき、図がかけないと手も足も出なくなります。
図は、水そうを正面から見た図で十分です。立体的な図をかくのはたいへんです。
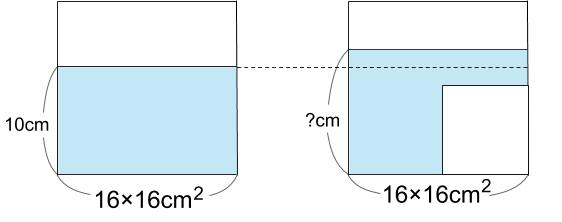

どうして水の深さは深くなったのか。
水が増えたから?

いいえ、水は増えてません。同じ量です。
水は移動しただけです。

そうだね。
水がもともとあった場所に、おもりがやってきた。
おもりが水を押し出したんだ。
水は、はじめの場所にいられなくなって、上の方に移動したんだね。
つまり、図の(クリーム色の部分の体積)と(おもりの体積)が等しいということです。
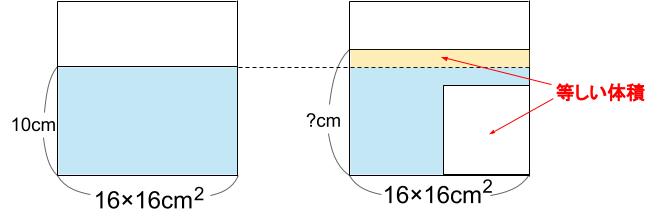

はい、わかります。
おもりの体積は、
8×8×8=512 \(cm^3\)
クリーム色の体積も512 \(cm^3\) だということだから、
512÷(16×16)=2
つまり、クリーム色の部分の高さが2cm。
水位は、
10+2=12
12cmです。
求まりました!

正解です。

ここで、このタイプの問題を解くときのコツを伝授します。
今回は、「2つのものが等しい」
ことがポイントでした。
(おもりの体積)と(クリーム色の部分の体積)が等しかったですね。
そして、「2つのものが等しい」ということを、
等式で表します。
おもりの体積は、8×8×8 \(cm^3\)
クリーム色の部分の体積は、16×16×□ \(cm^3\)
※高さを□としています。
この2つは等しいので、下のような等式になります。
8×8×8=16×16×□

はい、わかります。
あとは逆算で□を求めるのですよね。
8×8×8=512
16×16=256
だから・・・

いやいや。
そんな面倒な計算はしないでください!!
「等式」はどんどん簡略化していくのです!
等式の簡略化の例を下に示しますよ。
8×8×8=16×16×□
左も右も8で割ると、
1×8×8=2×16×□
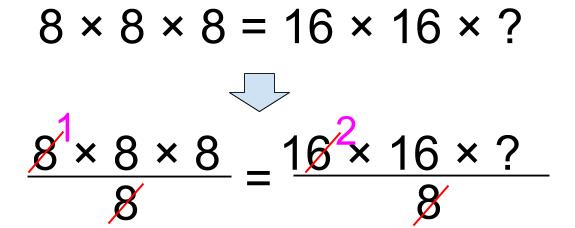

「等しい」を保ったまま、式を簡単にしていくのです。
左にも右にも同じ計算をすれば、「等しいまま」ですからね。

1×8×8=2×16×□
さらに、左も右も8で割ると、
\(\displaystyle \frac{1×8×8}{8}\)=\(\displaystyle \frac{2×16×?}{8}\)
つまり、
1×1×8=2×2×□

なるほど。
もう暗算でわかります。
1×1×8=2×2×□
□=2
簡単な計算で済みますね。

今回は「等式の簡略化」をしないで、ただただ計算をしても、それほど面倒ではない数値だけどね。
「等式の簡略化」をすると、計算が楽になるありがたみはわかるよね。
桁数の大きな筆算をしないで済む可能性がとても高いし、暗算ですいすいと計算が進む。
等式の利用は、いろいろな単元で使う重要な計算テクニックです。
しっかりと身につけましょう!
とりわけ、水そうの問題では、ものすごく良く使うからね!
