水そう
水位のグラフ
例題1
下図のような直方体の水そうがあります。水そうの左下には、直方体のおもりがぴったりとはまるように置いてあります。また、グラフはこの水そうに毎分一定量の水を入れたときの、水を入れ始めてからの時間と水の深さとの関係を表したものです。
(1)毎分何Lの水を入れていますか。
(2)図とグラフのア、イ、ウの値を求めなさい。
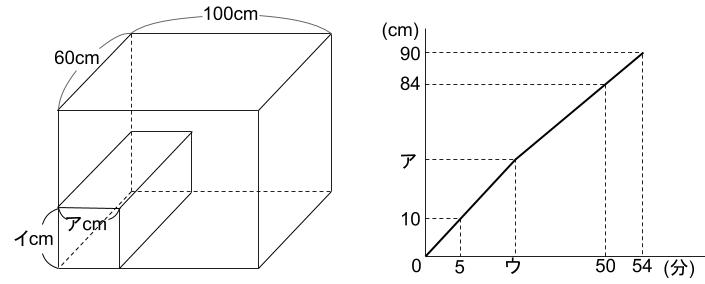
解説
(1)毎分何Lの水を入れていますか。

まずはグラフから読みとれることを図で確認しておきましょう。
0分から5分です。
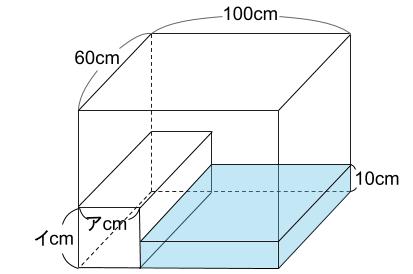

次に、50分から54分です。
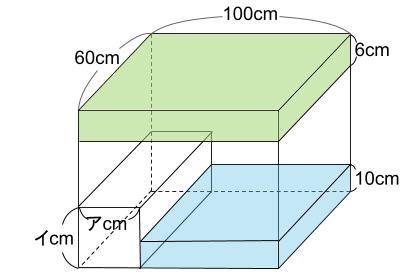

体積が求まるのは、50分から54分の緑色の直方体ですね。
100×60×6 \(cm^3\) を、4分なので
100×60×6÷4=9000 \(cm^3\)
9Lです。

はい、正解です。
(2)ア、イ、ウの値

さて、今までのように「広さを比べて解く」方法でいきましょうか。
まず、下と上を比べやすくするために、「高さ」をそろえましょう。
何cmにそろえても良いです。
今回は、下部分を0.6倍して、高さを6cmにそろえてみましょう。
かかる時間も0.6倍ですね。
5×0.6=3分です。
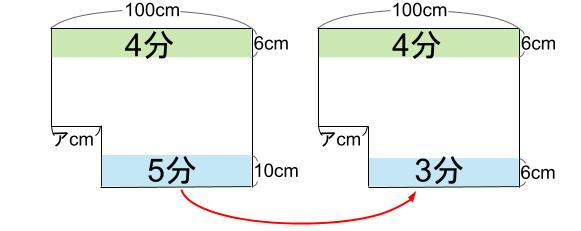

そして、今までのように
「もし、出っ張っていなかったら」
上の部分が、2つに分かれます。
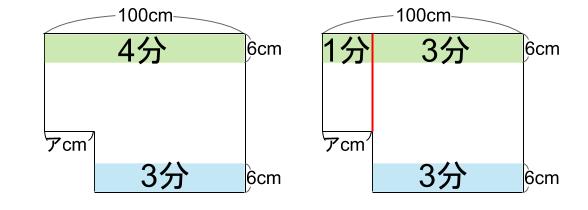

なるほど。
これでアが求まります。
左が1分。
右が3分。
左の3倍の広さが右です。
100cmが④で、①と③に分ければよい。
①が25cmで③が75cmです。
ア=25ですね。
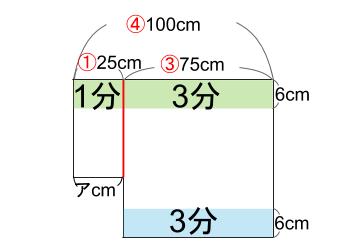

はい、正解です。
次にイとウを求めます。
もしも出っ張っていなかったら・・・
90cmの水位になる時間を求めます。
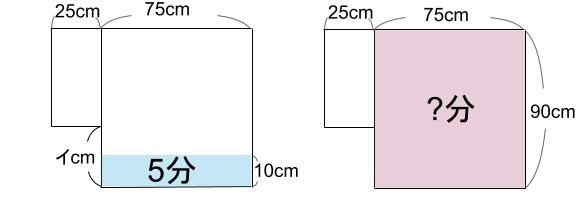

90cmは10cmの9倍なので、
5×9=45
45分です。

そうですね。
そして、本当は出っ張っていて、90cmの水位になった時間は54分。
つまり、54-45=9
出っ張り部分は、9分で満水になる体積です。
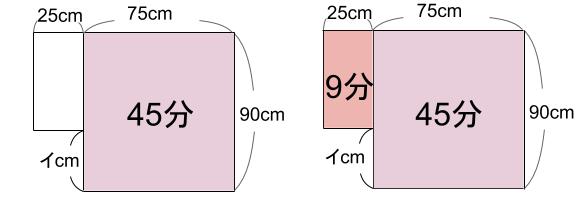

なるほど・・・
次は、えっと・・・

上の部分が、25cmと75cmにわれているでしょ。
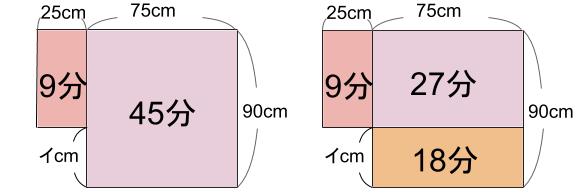

ああ!
9分の3倍は27分。
45-27=18分
なるほど!

27分は18分の \(\displaystyle \frac{27}{18}\)=\(\displaystyle \frac{3}{2}\) 倍
だから、
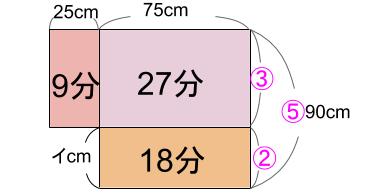
90cm=⑤として、
これを②と③に分ける。
①が、90÷5=18なので、
イ=②=36
ですね。

はい、正解です。

あとはウですね。
グラフより、
5分で10cm水位があがる。
36cm水位があがる時間は、36÷2=18
18分です。
ウ=18と求まりますね。

はい、正解です。
別解

速さのつるかめ算として処理することもできます。
第1ステージでは毎分2cm
第2ステージでは毎分1.5cm
54分で90cm水位が上がりました。
つるかめ算により、
2×18 +1.5×36=90
より、ウ=18と求められます。
また、「速さ」の問題としてとらえるならば、つるかめ算ではなく「速さと比」に着目して解くことも可能です。
