水そう
水位のグラフ
例題1
下図のような直方体の水そうがあります。水そうの左下には、直方体のおもりがぴったりとはまるように置いてあります。また、グラフはこの水そうに毎分一定量の水を入れたときの、水を入れ始めてからの時間と水の深さとの関係を表したものです。
(1)毎分何Lの水を入れていますか。
(2)図のアの値を求めなさい。

解説
(1)毎分何Lの水を入れているか。

はじめてのタイプですね。
まずは、水そうとグラフの関係について、先生といっしょに見ておきましょう。
第1ステージです。0分から16分です。
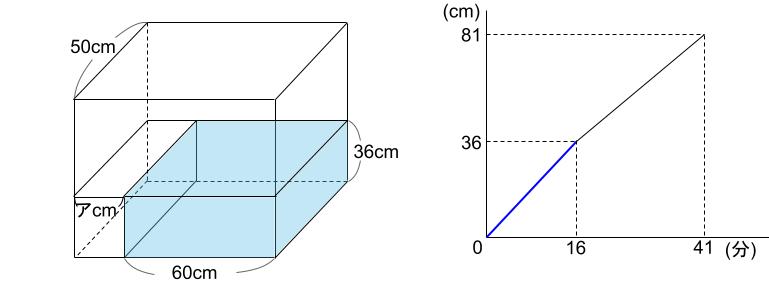

第2ステージです。16分から41分までの25分間です。
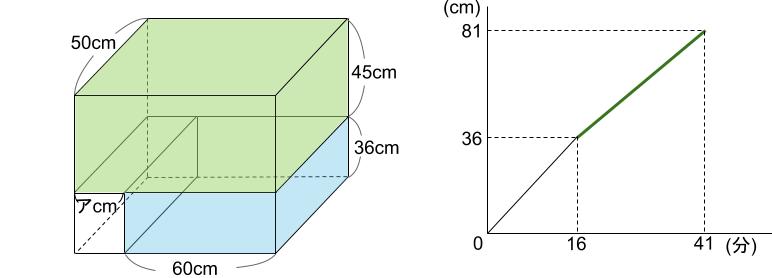

1分あたりの入水量ですが、
第1ステージの直方体が16分で満水になった。
第2ステージの直方体が25分で満水になった。
のどちらかから求められます。

直方体の体積が求められるのは第1ステージですね。
第1ステージを16分だから、
60×50×36×\(\displaystyle \frac{1}{16}\)=6750 \(cm^3\)
毎分6.75L入れています。

正解です。
(2)図のアの値

まだ使っていない第2ステージに着目しましょう。
緑色の直方体の体積は、
(60+ア)×50×45 \(cm^3\)
であり、
この部分を毎秒6750 \(cm^3\) で25分です。
よって、等式にします。
(60+ア)×50×45=6750×25
左右を25で割って、
(60+ア)×2×45=6750
左右を5で割って、
(60+ア)×2×9=1350
左右を9で割って、
(60+ア)×2=150
ア=15
と求まりました。

はい。体積を2通りで表せるから、等式ですね。

ところで!
今までのように「広さを比べて解く」こともできます。
やはり、こちらの方が簡単なことが多いです。
正面から見た図です。
グラフから第1ステージが16分
グラフから第1ステージが25分
次の図のようになります。
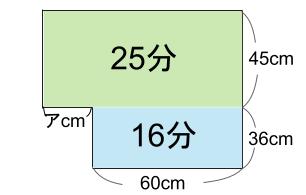

上と下の横の長さが同じならば、とても比べやすいのです。
上の部分が、もし、左に出っ張っていなかったら・・・
これで解くのです。!
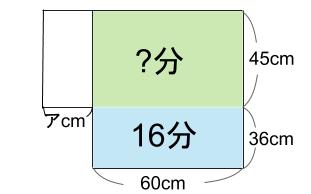

緑の部分は何分かかりますか?

16分の \(\displaystyle \frac{45}{36}\) 倍なので、
16×\(\displaystyle \frac{45}{36}\)=20
20分ですね。

そうですね。
上部分は本当は25分かかっているので、
左の出っ張り部分は、25-20=5分です。
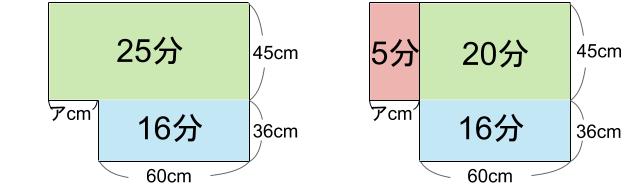

赤が5分
緑が20分
広さは\(\displaystyle \frac{5}{20}\)=\(\displaystyle \frac{1}{4}\) 倍です。
60×\(\displaystyle \frac{1}{4}\)=15
ア=15
求まりました。
なるほどー!

正解です。
