水そう
水位のグラフ
例題1
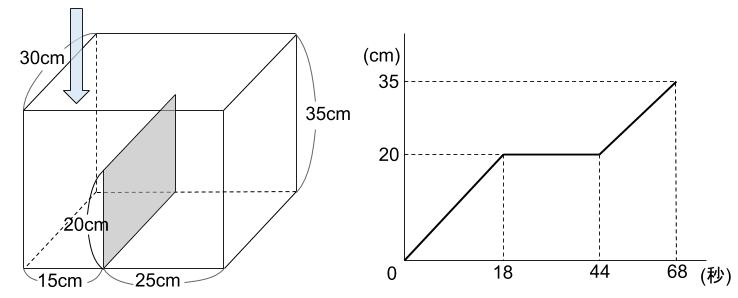
下図のような、しきりのある水そうの左側から、毎秒一定量の水を注ぎました。途中から入れる水の量を1.5倍に変えて水そうがいっぱいになるまで水を入れました。このとき、最も深いところではかった水の深さと水を入れた時間との関係は下のグラフのようになりました。
水を入れる量を1.5倍に変えたのは、水を入れ始めてから何秒後か求めなさい。ただし、しきりの厚さはないものとします。
解説

難しいですね・・・
わからないです。

第1ステージや第3ステージの途中で水量を変えたならばグラフの概形は下のようになります。
よって、第2ステージのどこかで変えたことがわかります。
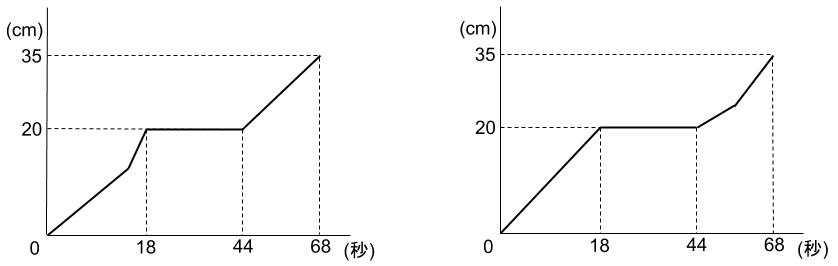

確かにそうですね。
なるほど。

いつも通り、正面から見た図で処理をしましょう。
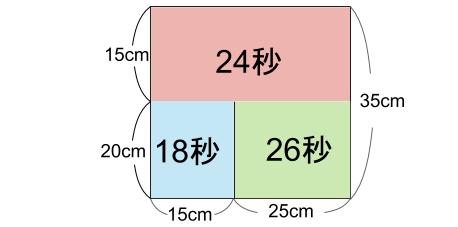

今までは、ここから広さ比べをしていました。
今回は、途中で入水量を変えているのですから、水を入れた時間では広さ比べはできません。
3か所の体積は、時間だけを見ても正しく比較できないのです。

はじめの入水量を②
途中から1.5倍の③に変えたとします。
第1ステージはずっと②ずつ入れます。②×18=㊱
第2ステージのはじめは②、途中から③ずつ入れます。
第3ステージはずっと③ずつ入れます。③×24=◯72
第1ステージと第3ステージの体積(水量)が求まります。
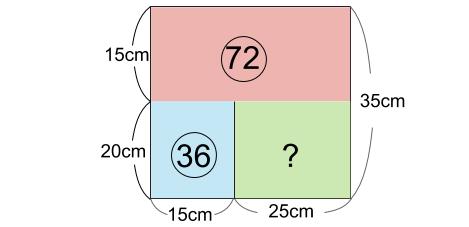

第2ステージは、
第1ステージの、\(\displaystyle \frac{25}{15}\) 倍
36×\(\displaystyle \frac{25}{15}\)=60
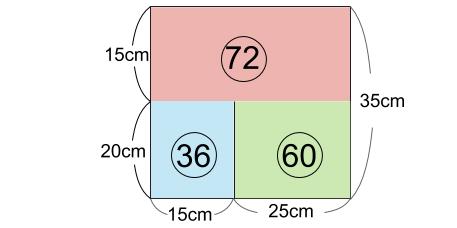

第2ステージのはじめは②、途中から③ずつ入れます。
②で?秒
③で?秒
合計26秒で〇60入った。

これはつるかめ算ですね。
つるかめ算を解いて、
②×18+③×8=〇60
と求まります。
つまり、第2ステージのはじめの18秒までは、はじめと同じ水量だった。
18+18=36
入水量を変えたのは36秒後です。

はい、正解です。
