水そう
水位のグラフ
例題1
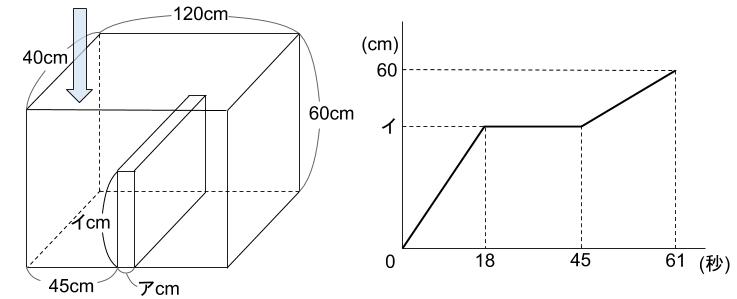
下図のような厚みのあるしきりを置いた水そうの左側から、毎秒一定量の水を注ぎます。このとき、最も深いところではかった水の深さと水を入れた時間との関係は下のグラフのようになりました。
図とグラフの、アとイにあてはまる値を求めなさい。
解説

しきりに厚みがあります。
いつも通り、正面方向から見た図で処理をしましょう。

第2ステージは、45-18=27秒
第3ステージは、61-45=16秒
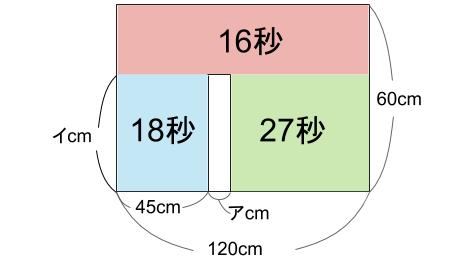

解き方は今までと同じですよ。広さ比べができる所を探します。

18秒と27秒ですね。
何倍なのか計算すると、
27÷18=\(\displaystyle \frac{27}{18}\)=\(\displaystyle \frac{3}{2}\) 倍の広さです。
つまり、横の長さが \(\displaystyle \frac{3}{2}\) 倍
45×\(\displaystyle \frac{3}{2}\)=67.5cm
さらに、しきりの厚さも求まります。
120-(45+67.5)=7.5cm
アが求まりました。
ア=7.5です。
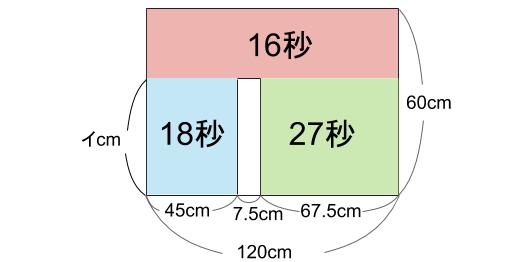

正解です。
続きはどうかな?

上と下の広さ比べ。
16秒と45秒は\(\displaystyle \frac{16}{45}\) 倍?
なんか違う気がする・・・

そうだね、違いますよ。
「もしも、仕切りがなかったら」
です。
つまり、45cmと120cmの広さ比べをします。
もしも、仕切りがなければ、ちょうど
\(\displaystyle \frac{120}{45}\)=\(\displaystyle \frac{8}{3}\) 倍の広さです。
18×\(\displaystyle \frac{8}{3}\) =48秒
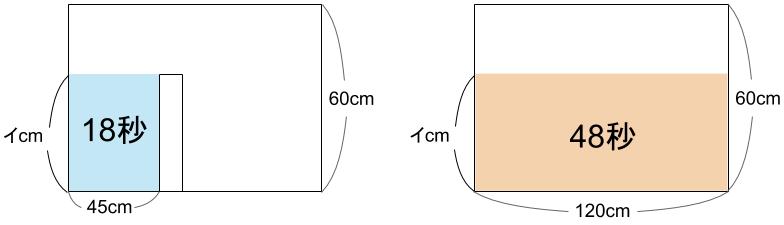

なるほどー。
あとは、上と下の広さ比べですね。
下が48秒
上が16秒
広さが、48÷16=3倍です。
つまり、高さが3倍です。
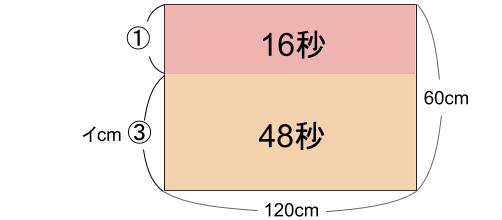

④=60cm
①=15cm
③=45cm
求まりました。イ=45です。

はい、正解です。
