水そう
水位のグラフ
例題1
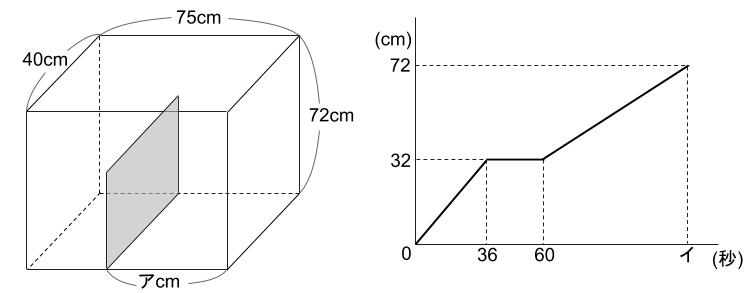
下図のようなしきりのある水そうの左側から、毎秒一定量の水を注ぎます。このとき、最も深いところではかった水の深さと水を入れた時間との関係を表したのが下のグラフです。
ただし、しきりの厚さはないものとします。
(1)水は毎秒何Lずつ注いでいるか求めなさい。
(2)図とグラフの、アとイにあてはまる値を求めなさい。
解説
(1)水は毎秒何Lずつ注いでいるか

水量は・・・・
どこに着目すれば求められるのか、迷う人がでるタイプの出題です。

えっと・・・
第1ステージは、体積が求められない。
第2ステージは、体積が求められない。
第3ステージは、体積がわかるけど、時間がわからない・・・

着目すべきは、第1ステージと第2ステージを合わせたものです。
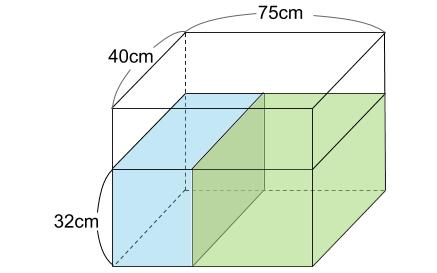

体積は、
75×40×32 \(cm^3\)
時間は、60秒。
なるほど!求められますね。
75×40×32 ×\(\displaystyle \frac{1}{60}\)=1600 \(cm^3\)
つまり、1.6Lです。

正解です。
入水量の求め方がすぐにわからないときは、一回飛ばして他の問題を解いてしまいましょうね。
入水量を使わないでも「広さ比べ」の解法で求められますからね。
そして、アやイの値がわかれば、入水量の求め方がわからないということもなくなりますし。
(2)アとイの値

水そうを正面から見た図をかきます。
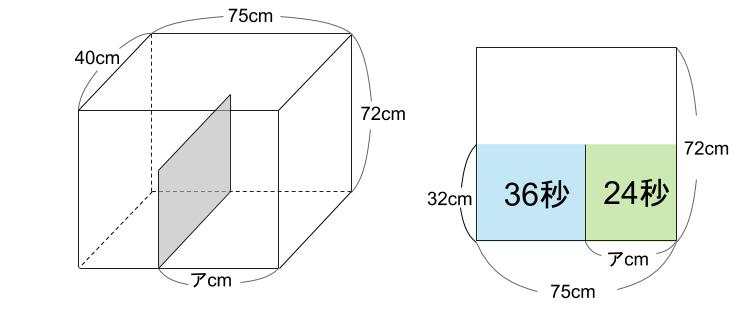

36秒と24秒。
広さ比べをします。右は左の何倍なのか。
24÷36=\(\displaystyle \frac{24}{36}\)=\(\displaystyle \frac{2}{3}\) 倍
で・・・次はどうするんだっけ?

\(\displaystyle \frac{2}{3}\) 倍
とは、3つに分けて、それが2つ分という意味だ。
下図のようになるよね。
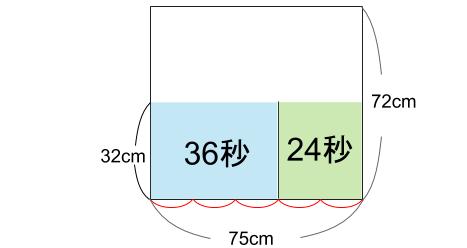

上図のように山をかいて分けるのは、数値によってはとてもたいへんだ。
\(\displaystyle \frac{13}{20}\) 倍とかね。
20山とか13山とかかくのはイヤだよね。
このようなときは、②とか③のような、〇数値を使うのです。
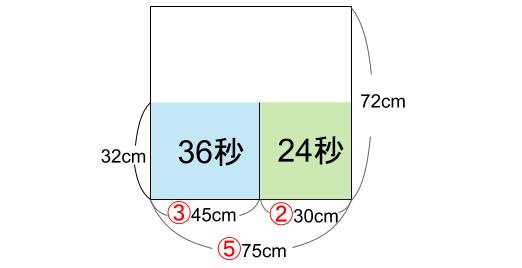

⑤=75cmだから、
①=75÷5=15cm
②も③も求まりますね。なるほど。
ア=②=30
30cmですね。

はい、正解です。
次にグラフのイ秒を求めましょう。

第3ステージですね。
これは、「もしも、しきりがなかったら」ですね。
覚えましたよ!
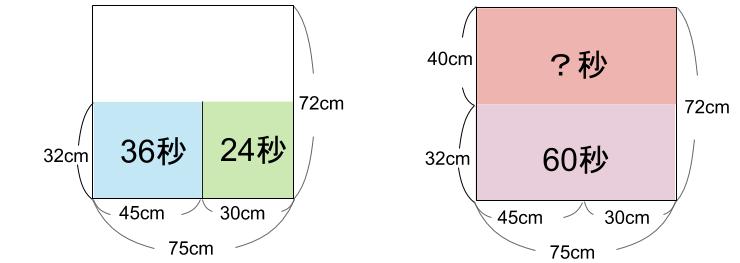

60秒で32cm
では、何秒で40cmになるか。
「60秒で32cm」
を4で割れば、
「15秒で8cm」
8cmを5倍すれば40cmだから、
「75秒で40cm」
第3ステージに水を入れる時間は、75秒です。

よいですね。
比例を上手に使えています。
分数を使って一発で計算するならば、
40cmは32cmの、\(\displaystyle \frac{40}{32}\) 倍
水を入れる時間も\(\displaystyle \frac{40}{32}\) 倍なので、
60×\(\displaystyle \frac{40}{32}\)=75秒
分数にもどんどん慣れていって欲しい。

分数ですね。なるほど。

さて、イの値は75ではないね。
60+75=135
イは135です。
