水そう
水位のグラフ
例題1
下図のような高さが20cmのしきりがある水そうの左側から、毎秒0.4Lの水を注ぎます。このとき、最も深いところではかった水の深さと水を入れた時間との関係を、グラフに表しなさい。ただし、しきりの厚さはないものとします。
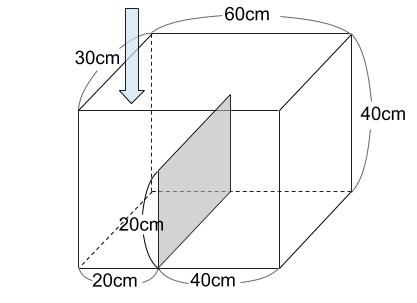

解説
第1ステージ

はじめての問題です。
どのようになるか、先生が説明をしていきますね。
まず左の直方体部分が満水になります。
ここを第1ステージとします。
第1ステージの体積は、20×30×20=12000 \(cm^3\)
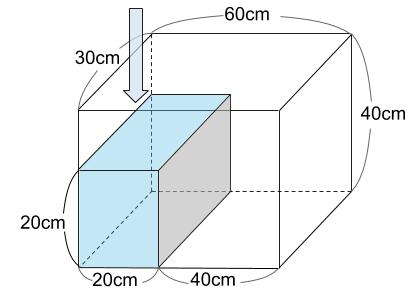

第1ステージに水の入る時間を求めましょう。
毎秒0.4L=400 \(cm^3\) の水を入れるので、
12000÷400=30秒
もちろん、分数を使ってまとめて計算するのが良いでしょう。
20×30×20×\(\displaystyle \frac{1}{400}\)=30秒
これをグラフにします。

第2ステージ

次に、水は右側にあふれていきます。
これを第2ステージとします。
わかりやすさのために色を変えます。緑色の部分です。
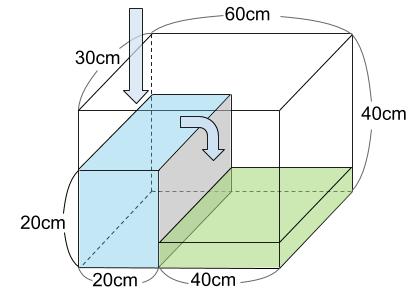
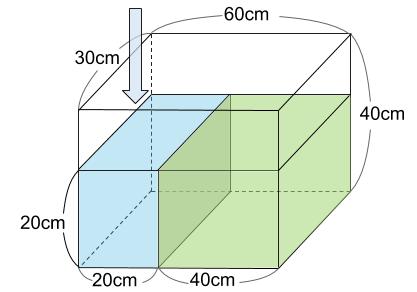

第2ステージの体積は、40×30×20=24000 \(cm^3\)
かかる時間は、
24000÷400=60秒
もちろん、まとめて計算するのが良いでしょう。
40×30×20×\(\displaystyle \frac{1}{400}\)=60秒
グラフにします。
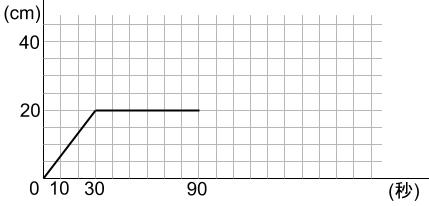

最も深いところではかった水の深さをグラフにします。
第2ステージに水が入っている間、ずっと20cmのままになります。
ところで・・・
今求めた、「第2ステージが満水になる時間=60秒」なのですが、
もっと簡単に求められますよね?
分かりますか。?

?
わからないですよ・・・


第1ステージと第2ステージの広さを比べます。
第2ステージ(右)は第1ステージ(左)何倍の広さですか?

横の長さが、20cmと40cm。
他はすべて同じ。
40÷20=2
2倍ですね。
2倍の広さです。

そうですね。2倍の広さです。
だから、水を入れるのにかかる時間も2倍になります。

第1ステージが30秒だっだから、
第2ステージはその2倍、30×2=60秒か。
なるほど!

そういうことです。
体積を計算しなくとも、「広さ比べ」をすることで解決できます。
例えば、
広さが3倍なら、かかる時間も3倍。
広さが1.5倍なら、かかる時間も1.5倍。
広さが \(\displaystyle \frac{2}{3}\) 倍なら、かかる時間も \(\displaystyle \frac{2}{3}\) 倍。
整数倍だけでなく、分数倍であっても成り立ちます!
第3ステージ

さて、いよいよ最後のパートですね。
第1ステージと第2ステージの上の部分に水が入っていきます。
ここを第3ステージとします。
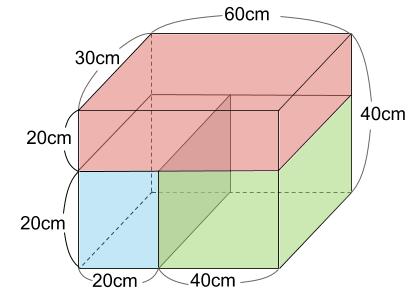

この部分の体積は、30×60×20=36000 \(cm^3\)
かかる時間は、
36000÷400=90秒
ここだってもちろん、まとめて計算するのが良いでしょう。
30×60×20×\(\displaystyle \frac{1}{400}\)=90秒
グラフにすると下のようになります。
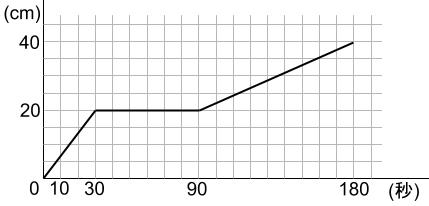

この第3ステージも、もっと楽に解ける方法があります。
「広さ比べ」です。
そのためには、「もしも、しきりがなかったら?」を考えるのです。

もしも、しきりがなかったら・・・
普通の水そうですね。
グラフもただの一直線ですね。

そういうことです。
まずは、空の状態から深さ20cmになるまでを考えましょう。
しきりがなかったら、空の状態から深さ20cmになるまで、何秒かかるか。
面倒な計算をしなくてもわかりますね?
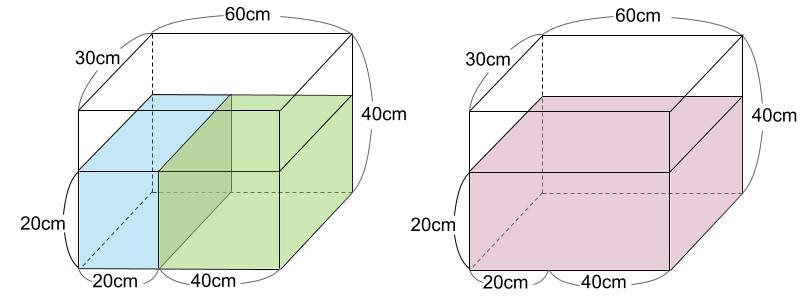

しきりがあったとき、
第1ステージに30秒
第2ステージに60秒
合計90秒かかって深さ20cmまで水が入りました。
仕切りがなくたって同じです。
同じ水量を入れるのにかかる時間は90秒です。
この仕切りなし水そうの水位の変化を、先のグラフに重ねて赤線で書き入れると下のようになります。
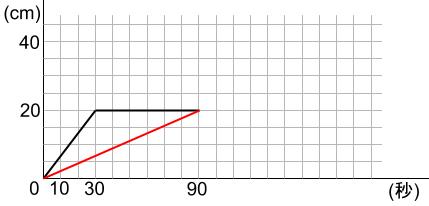

なるほど。
そういうことになりますね。

このあと、さらに水を入れていきます。
水位はどう変化するのでしょうか。
グラフはずっとかわることなく伸びていくことがわかりますね?
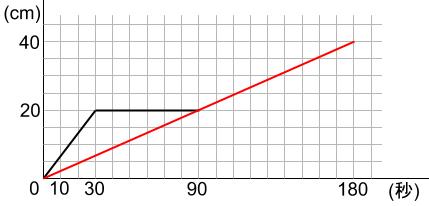

なるほど。
簡単ですね。

「広さ比べ」の解き方。
「もしも、しきりがなかったら?」という見方。
しっかり覚えて使いこなしていきましょう!
