水そう
水位のグラフ
例題1
下のグラフは、図のような直方体の容器に、一定の割合で水を注いだときの、時間と水の深さの関係を表したものです。
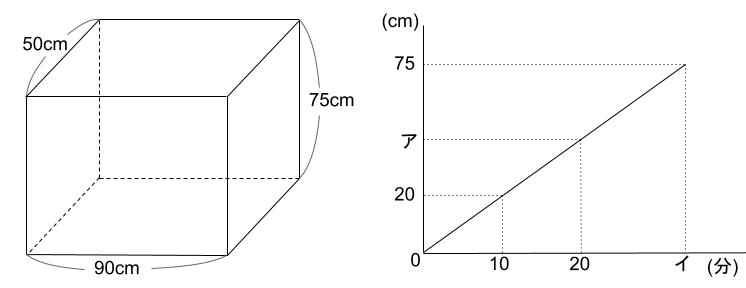
(1)水は毎分何Lずつ注いでいるか求めなさい。
(2)グラフの、アとイにあてはまる値を求めなさい。
解説
(1)水は毎分何Lずつ注いでいるか


10分後の図です。
グラフから水位は20cmです。
このときの水量は、
90×50×20=90000 \(cm^3\)
1L=1000 \(cm^3\)
なので、
90000 \(cm^3\)をリットル(L)になおすと、
\(\displaystyle \frac{90000}{1000}\)=90
水量は90Lです。

10分かけて90Lの水を入れたのですから、
1分あたりの水を入れた量は、
90÷10=9
毎分9L入れました。

はい、そういうことです。
正解です。
(2)アとイの値

アを求めるのに「毎分9Lずつ水を入れた」という情報は必要ありませんね。
10分で20cmなのですから、
20分で40cmです。
下図からあきらかでしょう。
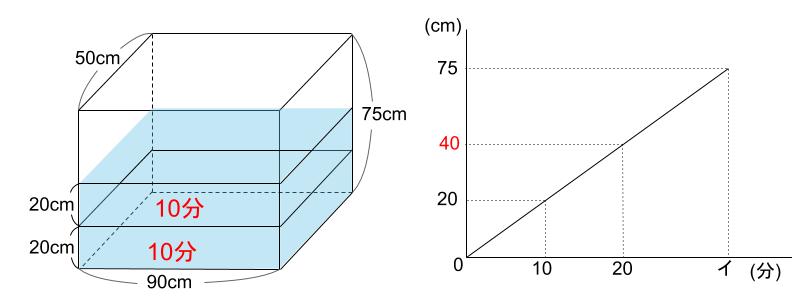

なるほど。
簡単に求まりますね。
ア=20ですね。

続いてイを求めましょう。
イを求めるのに「毎分9Lずつ水を入れた」という情報は必要ありませんね。
グラフだけ見て解くことができます。

10分で20cmだから、
1分で2cmです。
75÷2=37.5
75cmの水が入るには、37.5分かかります。
イ=37.5
求まりました。

はい、正解です。
保護者さまへ
もちろん、「毎分9Lずつ水を入れた」という情報を使って、ア、イを求めることもできます。しかし、「比例」という最も重要な感覚を身につけさせましょう。
「整数倍」ならば、ほぼすべての子が身についています。
「分数倍」をいかに身につけさせるかが最重要事項です。
これこそが「割合・比」であり、中学受験算数の柱です。
