1:線分図の導入
1:和差算と線分図
和と差が与えられました。もとの数を求めなさい。これが和差算です。
つまり、
A+B=100
A-B=50
さてAとBはいくつですか、というタイプの問題です。
和差算は6年生になる頃には、単独で出題されるというよりも、他の問題の中で使用する基本的な計算技術です。しっかりマスターしましょう。
※中学受験算数全体におけるポジションは、線分図の導入のための基礎問題ともいえます。4年生の初期に、算数ってパズルみたいだなあと思ってもらうきっかけとなる問題の1つです。
例題1
4mのロープを切って2つに分けました。長い方は短い方より60cm長いとき、長い方のロープは何㎝ですか。
解説
まったく何も教えないで、自力で解かせてみたい問題です。子どもが自分で、様々に挑戦するようならば、正解をだせなくとも算数の素質がある子どもと言えます。
本単元の目的は「線分図の導入」なのですが、例題1は「線分図」を使わずに工夫して解くことも可能です。後ほど「研究」にて紹介します。

さあ、今日も楽しく算数をしよう。

今日の問題はめちゃくちゃ簡単な予感がします。

ほんと?では、さっそく解いてもらおうかな。

まず半分に切る。
400÷2=200
60cm長いので足す。
200+60=260
長い方は260cmですね。

確かめてごらん。確かめは計算の見直しじゃなくて、問題の条件をと合っているかの確かめだからね。

400-260=140
短い方は140cm
あれ、長いロープは短いロープより80cm長いな・・・
260-140=80だもの・・・
間違ってる・・・

確かめをすることで、自分の間違いに気がつけるってすごく重要だよ。
問題の意味がしっかりわかっていないとできないからね。

でも間違いだったからね。
さてどうやったら解けるのかな?
文章題は、矛盾がないかどうかの確認をさせる良い機会になります。
矛盾があれば間違っている。このような考え方を身につけさせましょう。
※ただし、5年生の中盤位まで、この考え方が身に付かない子もいるようです。
成長段階に合わせて、無理を強いないようにしましょう。

あてはめで探すか、図で整理してみるか・・・

図にしてみると・・・・
!!!先生!!!緊急事態です!!この問題
具体図がかけません!!!

そんなにあわてないでよ。
今日の問題から学ぶことの1つ目
「具体図がかけない問題があるぞ」
に到達したね。
エライ!

デヘヘ、それほどでもないっすよ!

調子にのるなよ、そんなにはエラクないぞ。
さて、今回は先生から教えてしまうぞ。
この問題には線分図という図がとても相性が良いのだ。
こんな図だよ。
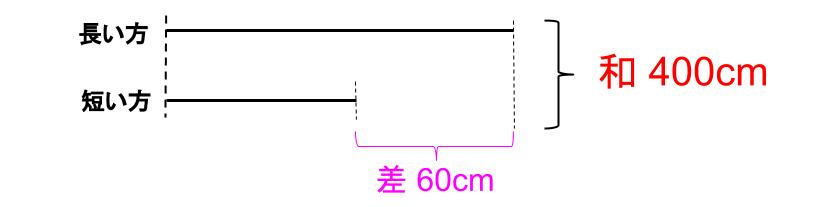

なるほど。2つのロープの差をうまく表せていますね。
400-60=340
短い長さが2つ分で340㎝だ。
340÷2=170
短いほうは170㎝
長いほうは230㎝
答えは230cmです。
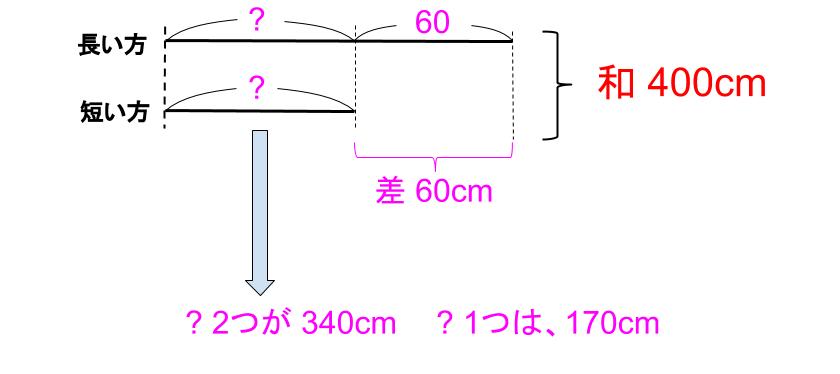

この答えは、問題の2つの条件とうまくいっていますね。
今回のように2つの数の和と差から、元の2つの数を求めるものを和差算といいます。
算数では和と差に着目することがとっても多いですよ。

線分図かあ。和差算は線分図で解くんですね!

「~算」は「~図」で解く、という暗記はしないでね。
問題文を読んで、「その問題にあった図は何かな」という頭の使い方を
しようね。
もちろん結果的に、和差算は線分図で解くのがおススメなんだよ。
それは間違いじゃない。
ただし、テストや入試では、問題に「和差算」っていうタイトルはついてないからね。
たくさん練習を積めば、最終的には問題を読んで「あ、和差算的な状況だ、線分図を選ぼう」
という思考を極めて短時間で行うことになります。
このとき、自分でも考えて解いているのか、解き方を暗記しているか、判別はつきません。深い理解と暗記は混然一体となっていますので、一概に暗記を否定するのものではありません。
線分図を知らない子どもでも、独力で解くことが可能です。
数のあてはめです。あてはめを侮ってはいけません。
数学的思考につながる下地となります。
また、わからない問題でもガンガン立ち向かうという姿勢を育みます。
教えてもらわないとできない、やらないというのでは、算数がものすごく得意な子になる資質は少ないと言えます。
あてはめ解法を紹介します。
以下のような考え方を使って答えを探すこともできます。
素晴らしい解法ですね。
・和が400の中で探す
長い方 200 201 202 ・・・ 230
短い方 200 199 198 ・・・ 170
差 0 2 4 ・・・ 60
差が2ずつ増えるので、差が60になるのは30(60÷2)増やしたときとわかります。
・差が60の中で探す
長い方 60 61 62 ・・・ 230
短い方 0 1 2 ・・・ 170
和 60 62 64 ・・・ 400
和が2ずつ増えていくので、和が400になるのは170(400 -60=340、340÷2=170)増やしたときとわかります。
