水そう
棒を入れる
例題1
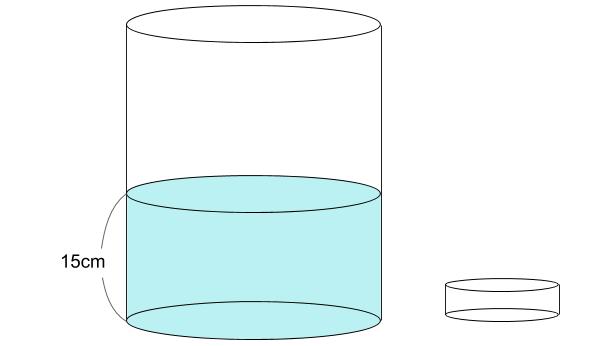
底面の半径が15cm、高さ40cmの円柱の形の容器に、水が15cmの深さまで入っています。この中に、底面の半径が7.5cm、高さ3cmの円柱の形の重りを、1個ずつ重ねて沈めていきます。円周率は3.14とします。
(1)重りを2個沈めたときの水の深さは何cmになりますか。
(2)重りを7個重ねて沈めたときの水の深さは何cmになりますか。
解説
(1)重りを2個

容器の底面積は、15×15×3.14 \(cm^2\)
おもりの底面積は、7.5×7.5×3.14 \(cm^2\)
何倍なのか計算すると、
\(\displaystyle \frac{15×15×3.14}{7.5×7.5×3.14}=4\)
だから、
容器の底面積は、④
おもりの底面積は、①
とおけます。

なるほど!
おもり2個を入れた図は下図のようになりますね。
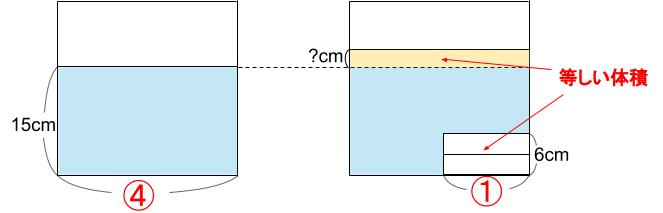

おもりの体積と、上がった水の体積が等しい。
①×6=④×?
?=1.5cm
水位は15+1.5=16.5
16.5cmです。

はい、正解です。
(2)重りを7個

おもり7個を重ねた高さは、7×3=21cm
水に全部沈まなそうですね。
下図のようになると予想します。
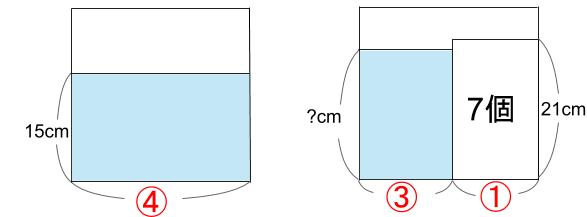

水の量は、おもりを入れる前と後で等しいので、
④×15=③×?
?=20
水位は20cmで、これはおもりの高さ21cmよりも低い。
つまり、上図の予想が正しいことになります。
答えは20cmです。

はい、正解です。
ここで計算した水位が、おもり7個の高さより高いときは、予想が外れたってことだね。
そのときは、おもりは全部沈んでいるので、その場合で計算をやりなおします。
