水そう
棒を入れる
例題1
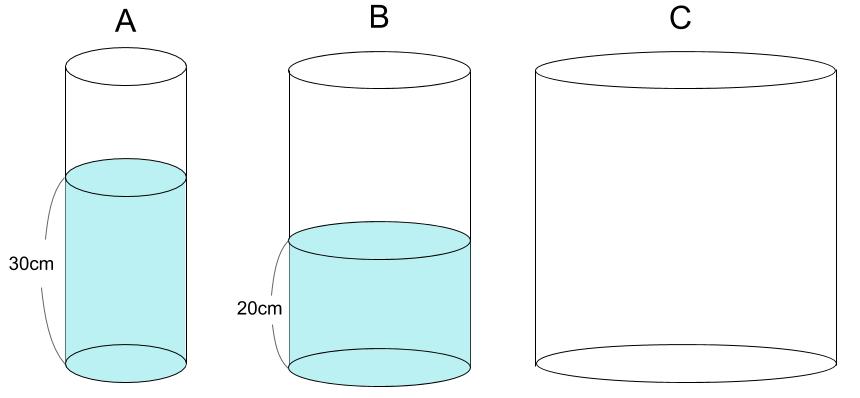
下図のような円柱の容器、A、B、Cがあります。底面の半径は、Aが4cm、Bが6cm、Cが10cmです。また、Aには水が深さ30cmまで、Bには水が深さ20cmまで入っていて、Cは空です。この水を、すべてCに移すと、水の深さは何cmになりますか。
解説

この問題も、底面積を具体的な値で処理する必要はないです。
やってみてください。

Aの底面積は、4×4×3.14=16×3.14
Bの底面積は、6×6×3.14=36×3.14
Cの底面積は、10×10×3.14=100×3.14
だから、
Aの底面積は、16
Bの底面積は、36
Cの底面積は、100
とおけます。

良いですね。3.14倍は全部省略できますね。
つまり、「具体的な底面積」ではなく「具体的な底面積÷3.14」で解いていくということですね。
さらに4で割って数値を簡単にしましょう。
つまり、「具体的な底面積÷3.14÷4」です。
Aの底面積は、4
Bの底面積は、9
Cの底面積は、25
これで解いていきましょう。
保護者さまへ
比や面積比を習ったあとならば、
A、B、Cの半径の比が、2:3:5なので、面積比は
(2×2):(3×3):(5×5)=4:9:25
と求めます。

Aの水量は、4×30=120
Bの水量は、9×20=180
水量の合計は、120+180=300
この水をすべてCに移すと、
25×?=300
より、
?=12cm
求まりました。

はい、正解です。
