水そう
水位のグラフ
例題1
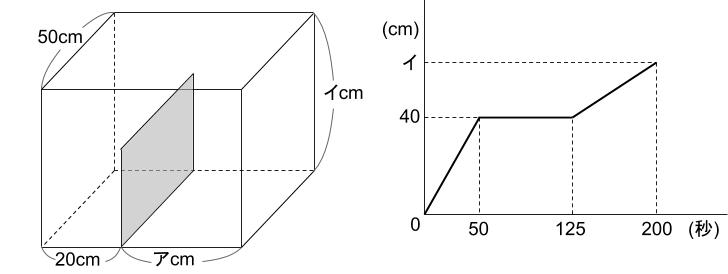
下図のようなしきりのある水そうの左側から、毎秒一定量の水を注ぎます。このとき、最も深いところではかった水の深さと水を入れた時間との関係を表したのが下のグラフです。
ただし、しきりの厚さはないものとします。
(1)水は毎秒何Lずつ注いでいるか求めなさい。
(2)図の、アとイにあてはまる値を求めなさい。
解説
(1)水は毎秒何Lずつ注いでいるか
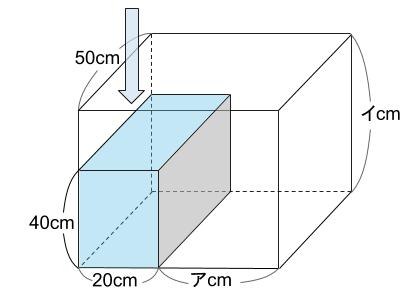

グラフから、しきりの高さが40cmであることがすぐにわかります。
また、第1ステージを満水にするのにかかった時間は50秒です。

第1ステージの体積を50秒で割れば、1秒あたりの水の量ですね。
20×50×40×\(\displaystyle \frac{1}{50}\) =800 \(cm^3\)
1秒で入れる水量は0.8Lですね。

正解です。
(2)アとイの値

アとイを求めるために、(1)で求めた入水量を使わない方法が楽です。
「広さを比べる解き方」ですよ。
下図のように、正面から見た図をかきます。
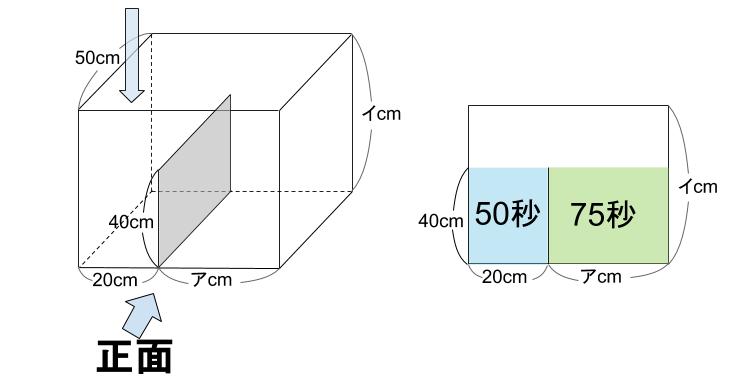

グラフより、
第1ステージ(左)は50秒
第2ステージ(右)は、125−50=75秒
75÷50=\(\displaystyle \frac{75}{50}\)=\(\displaystyle \frac{3}{2}\)倍
左の\(\displaystyle \frac{3}{2}\)倍の広さが右だ。
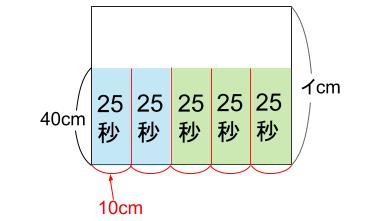

ということは、アは、
20×\(\displaystyle \frac{3}{2}\)=30
求まりました。30cmです。
ア=30です。

その通り。
正解です。
第1ステージと第2ステージは、高さが共通(40cm)、奥行も共通。
広さに違いが出るのは、横の長さの違いですね。

次にイを求めます。
第3ステージは、グラフより
200-125=75秒
で、「もしも、しきりがなかったら」
第1ステージと第2ステージは合わせて125秒
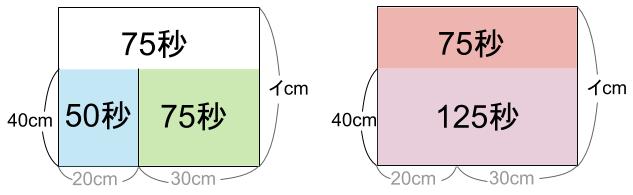

上と下の広さ比べをします。
上は下の何倍か求めます。
75÷125=\(\displaystyle \frac{75}{125}\)=\(\displaystyle \frac{3}{5}\) 倍
だから、
40×\(\displaystyle \frac{3}{5}\) =24cm
イ=40+24=64
求まりました。

正解です。
教えた通りうまくできましたね!
