1:旅人算やや応用
真ん中で出会う・その2
例題4
Aは学校から公園に向かって、Bは公園から学校に向かって、午前9時に同時に出発しました。2人は、公園と学校のちょうど真ん中にあるP地点より、180m公園に近いQ地点で出会いました。Aの進む速さが分速80m、Bの進む速さが分速60mのとき、学校から公園までの距離を求めなさい。
解説

あれ、何か簡単な気がします。
AとBの進んだ距離の差が180mになったときに出会った。
180÷(80-60)=9
つまり、9分後に2人が出会ったから、
(80+60)×9=1260m
学校から公園までは1260mです!

残念・・・間違いです。
もう、見事にこちらのねらい通りに間違えてくれましたね。
多くの子どもが、学くんと同じ間違いをするんだよ。

え?間違ってる・・・?

うん。きちんと図示をして解いてみてください。

図はこうなりますね・・・
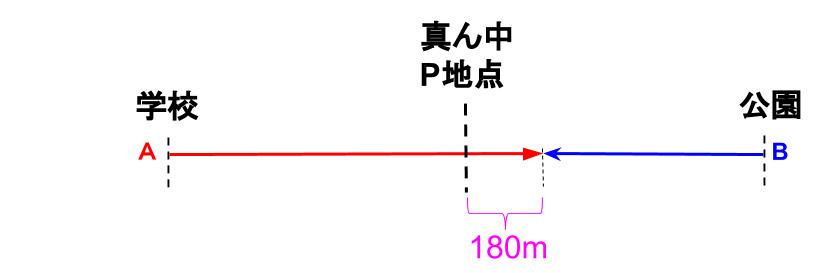

で?どうする?

今までやってきたのは、AとB2人の進んだ距離の和か、差に着目すれば解けました。
まず、和は・・・わからない。

うん、和はわからないで正解。

差は・・・180m

それがダメ。間違ってます。

?え・・・180mじゃないの?
えっと・・・

2本の線分の長さの差を取りたいのだよね。
線分図の頭をそろえてかくんだよ。
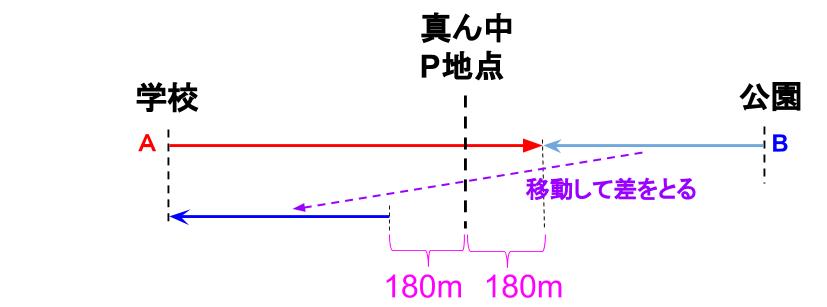

あ、AはBより、180×2=360(m)長い!
そうかあ。わかりました。
あとは、ただ計算するだけですね。
AがBより360m多く進むのは、
360÷(80-60)=18(分後)
2人は18分かけて出会ったのだから、
(80+60)×18=2520m
求まりました。2520mです。

OK!
正解です。
慎重に問題を整理して解かないといけないことがわかってくれたと思う。
何も考えずに適当に計算したって正解にはならない、しっかりていねいに解いていくことが大事なのだよ。

求めた値でうまくいっているか確かめもしておきましょう。
Aが18分で進む距離は、
80✕18=1440(m)
Bが18分で進む距離は、
60✕18=1080(m)
2520mのまん中は、2520÷2=1260(m)
2人のあった場所とまん中との距離は、
1440−1260=180(m)
1260−1080=180(m)
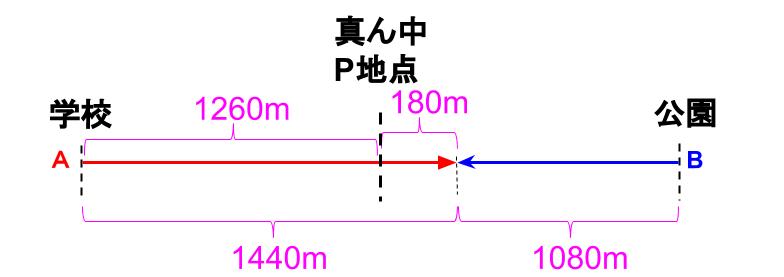

はい、確かにうまくいっていますね!
