1:旅人算やや応用
速さのつるかめ算
例題1
太郎は7時30分にP地点を出て分速250mで走ってQ地点に向かいましたが、疲れたので途中から分速80mで歩きました。すると7時51分にQ地点につきました。PQ間の距離が2700mとすると、太郎が歩きはじめた時刻は何時何分ですか。
解説
はじめてこの問題を与えられて、解けなくてもかまいません。習ってないから解けない、という子どもはたくさんいます。しかし、算数に対して自ら解き進める姿勢のある子は、この問題を習っていない問題とは思いません。自力で解く子もいるのが現実です。できれば、「速さのつるかめ算」というタイトルを見せないで、一度解かせてみたいものです。

あれ、登場人物が1人だ。
旅人算じゃないのかな?

そうかもしれないね。自力でやれるところまでやってみようか。

こんな図になりますね・・・


うん。何か気づけるかな?

わかんないです・・・全部で21分かかっています・・・

いいでしょう。
これは自力で気づけなくとも良しとする問題かな。
はじめてのタイプの問題なので、どんどん教えます。
これは「つるかめ算」で解けるんだよ。
どう?言われたら納得かな?

え?足もないし、1匹とか1個とかないけど・・・

「速さのつるかめ算」なのです。
7時30分から7時51分までの21分間、
もし、ずっと分速80mで進めば?

80×21=1680(m)進みます。

これは下図のような面積図で表せる。
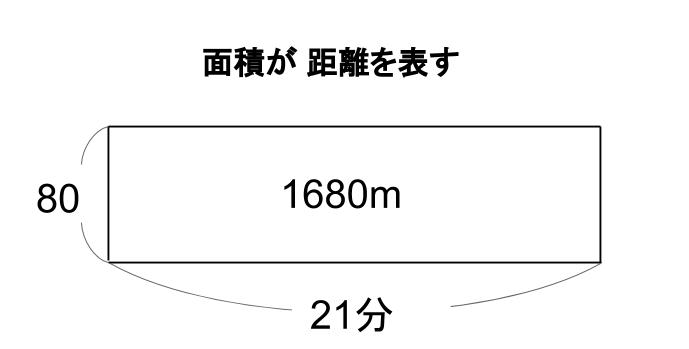

「たて(速さ)」×「横(時間)」=「面積(距離)」
ということです。
面積で、進んだ距離を表せるでしょ。
では、ア分間は分速250mで進み、イ分間は分速80mで進んだことを
面積図で表してみよう。
ア+イ=21(分)だよ。
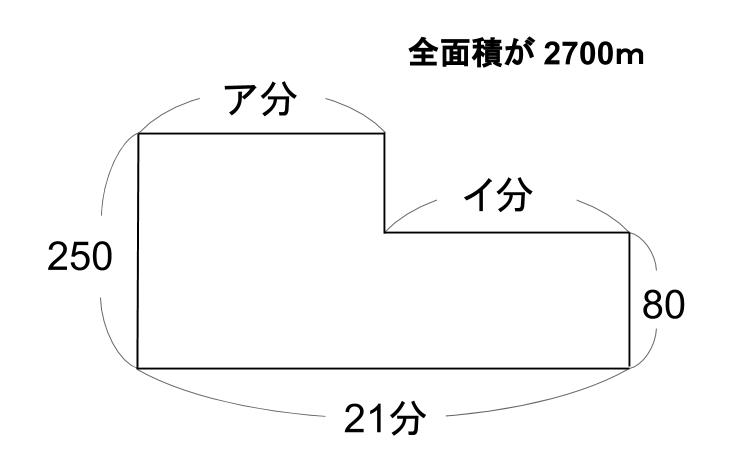

ああ、なるほど。確かにつるかめ算ですね。これ。
80×21=1680(m)
2700-1680=1020(m)
1020÷(250-80)=6
つまり、
分速250mで6分
分速80mで、21-6=15分
進んだ。
太郎が歩き始めたのは、スタートから6分後だから、7時36分です。

正解です。
分速250mで6分進めば、1500m
分速80mで15分進めば、1200m
合計21分で2700m進んだ。うまくいっていることが確かめられますね!
「つるかめ算」を使わない別解もあります。
ずっと分速250mで走った場合、
2700÷250=10.8
出発から10.8分後の7時40.8分にQ地点に着きます。
これは実際より10.2分早く着いたということです。
つまり7時40.8分に実際は、80×10.2=816m、Q地点の手前にいたことがわかります。
これだけの差が着くのは何分かかるのか、旅人算で求めることができます。
816÷(250-80)=4.8
つまり、7時40.8分までの10.8分間のうち、分速80mで4.8分進んだことがわかります。
10.8-4.8=6
このことから、分速250mで6分間すすんだことがわかります。
上の別解も素晴らしい解き方なのですが、おすすめはしません。
つるかめ算の方が簡単だからです。
つるかめ算の仕組みが問題文にでてきたら、反射的につるかめ算とわかるように訓練したいものです。
