【速さと比】通過算と比・その3

式処理がおススメだって教わりました。
式処理で解いてみます。

（距離）÷（速さ）＝（時間）
（電車の長さ）÷（時速50km－時速?km）=18秒
（電車の長さ）÷（時速60km－時速?km）=14秒

えっと・・・単位をそろえないといけないですね。
時速を秒速に直すか、
あるいは、18秒を \(\displaystyle \frac{18}{3600}\) 時間になおすか。

単位をそろえないと、正確な計算式にならない。
このことを意識できているのはとても素晴らしいことだね。

でもね、比の処理をするだけならば、単位は関係ないよ。
単位が「時間」でも「分」でも「秒」でも、比は一定ですからね。

電車の長さは同じだから、１：１
時間の比は、18：14＝９：７

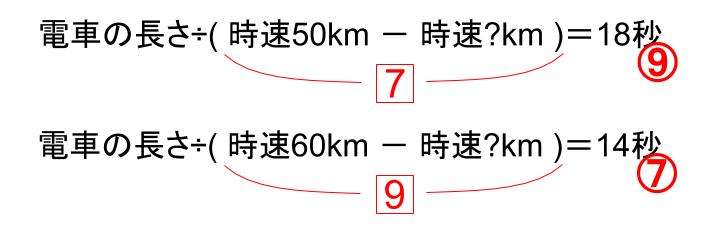
（距離）÷（速さ）＝（時間）
（電車の長さ）÷（時速50km－時速?km）=18秒
（電車の長さ）÷（時速60km－時速?km）=14秒

つまり、速さの部分の比は逆比の７：９になる。
長さ÷７＝18秒⑨　
長さ÷９＝14秒⑦　

だから、
（時速50km－時速?km）＝７
（時速60km－時速?km）＝９

２つの式の差をとれば、
２＝時速10km
だとわかります。

つまり、７=35なので、
（時速50km－時速?km）＝35
自転車の速さは、時速15km！
求まりました。

正解です。
では電車の長さを求めましょう。

電車の長さ÷（時速50km－時速15km）=18秒
なのだから、
電車の長さは、時速35kmで18秒進む長さ。

これこそは単位を無視できませんね。

18秒＝\(\displaystyle \frac{18}{3600}\) 時間＝\(\displaystyle \frac{1}{200}\) 時間

時速35kmで \(\displaystyle \frac{1}{200}\) 時間進む長さは、

35× \(\displaystyle \frac{1}{200}\) ＝\(\displaystyle \frac{35}{200}\) ＝\(\displaystyle \frac{7}{40}\)（km）
これをｍになおすから・・・

最後の約分、\(\displaystyle \frac{35}{200}\) ＝\(\displaystyle \frac{7}{40}\) はしない方がいいね。

長さの単位はｍで聞かれているので、1000倍が必要だ。

\(\displaystyle \frac{35}{200}\) ×1000 = 175ｍ　

こっちの方が計算が楽かな。
大差はありませんけども。

式処理で済ませてしまうのは確かに楽ですね。

式処理で済む問題だからだけどね。

定番を外れた状況ならば、図をかいて整理しないと解けない。
図が大事であることは間違いないんですからね。