通過算
人の前を通過
例題2
長さ90mの列車が踏切の前に立っている人の前を通り過ぎるのに6秒かかりました。この列車の時速は何kmですか。
解説

人の前を通過し始めた図からはじめます。


OK!
算数では特に断りにない限り、人は長さや厚みのないものとして扱う。
棒人間の図で考えるんだ。

次に、通過が終わったときの図をかく。
最後尾に着目すると・・・
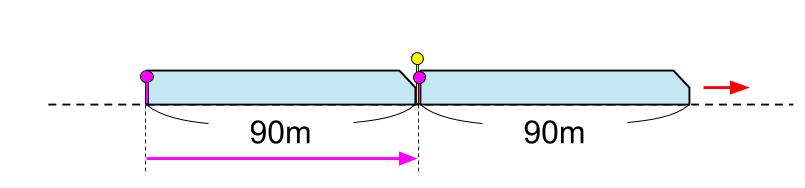

最後尾に乗る車掌に着目して、6秒で90m進んだことがわかります。
90÷6=15
秒速15mだ!

正解!
ちなみに、秒速ではなくて時速で聞かれているから、
15×3.6=54
だから、 秒速15m=時速54km
これが答えだね!

あとね、押さえておいて欲しいポイントがある。
「鉄橋の通過」と「人の通過」の仕組みはほとんど同じだってことだ。
「人」は「長さ0mの鉄橋」なのです。
そうすれば、2つの異なる問題ではなくて、同一の問題となります。
同じ考えで同じように解く問題だってことがわかってもらえればOKですよ。
時速と秒速の変換

通過算では、「時速90kmの電車が、10秒で通過」のように、「時速」と「秒」が非常に良く出てきます。
だから、時速を秒速になおしてから問題を解くことになります。
時速を秒速になおすことは、基礎の基礎の話題であって、改めてここで触れる必要のない話かもしれません。
でも、以下の代表的な時速と秒速は、覚えておいて損はありません。
というか、覚えましょう。
時速km 秒速m
36 10
54 15
72 20
90 25
108 30
全部丸暗記するというよりも、
時速36km = 秒速10m
を暗記しましょう。
あとは比例計算をするだけです。
時速36km = 秒速10m
を半分にすれば、
時速18km = 秒速5m
時速36km = 秒速10m
を1.5倍すれば、
時速54km = 秒速15m
すぐに求められるし、そんなに計算もたいへんではありませんね。
