異なる2種類の比の処理
問題中に異なる２つの比があるとき。共通部分で比をそろえて解くのが定番パターンでした。しかし、共通部分がない問題もあるのです。それらを見ていきましょう。
連比
例題１
ある学校の入学試験で、受験者の男女の比は４：５、合格した男子と不合格の男子の比は３：２、合格した女子と不合格の女子の比は７：３でした。不合格の男子が不合格の女子より６人多いならば、男子の不合格者は何人ですか。
解説
比が２つどころじゃないですね。３つありますよ。
異なる比が３つあります！
そうだね。
とにかく情報整理をしてみましょうね。
３つの比があるから、３つの記号です。
さて、ここから先は立ち止まるところではないよ。
進むべき道は完全に決まり切っているからね。
１．異なる比の共通部分が見つかれば、そこから比をそろえる。
２．共通部分が見つからないならば、等式をたてて消去算
この２つのことを考えるのです。
この２つのことを考えればよい、ということは暗記してくださいね。
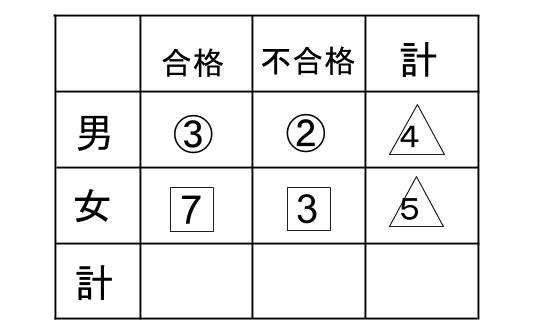
男子の合計は、⑤であり、△４ですね。
それに、
女子の合計は、10であり、△５です。
共通部分が２つ見つかりました。
その通り！
どちらからでもいいから、順にそろえていきましょう！
男子の合計、⑤＝△４からそろえます。
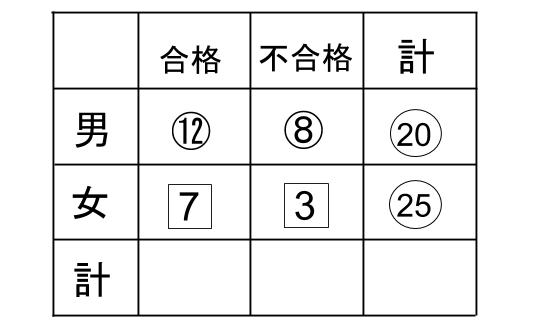
あらためて、男子の合計を⑳として、かきなおしてみます。
受験者の男女の比は４：５だから、⑳と○25
合格者した男子と不合格の男子の比は３：２だから、⑳を３：２にわけて、⑫と⑧
次に、女子の合計。
10＝○25
あらためて、50
としてかきなおします。
合格者した女子と不合格の女子の比は７：３だから、35と15
ここまでバッチリですよ！
「不合格の男子が不合格の女子より６人多い」とあるから・・・
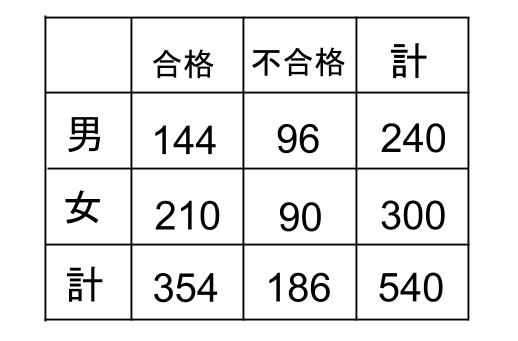
不合格者の男子16
が不合格の女子15
より、１＝６
不合格者の男子は16＝96
求まりました。96人です！
正解です！
複雑そうに見えて、けっこう単純だったでしょ。
消去算も不必要なパターンでした。
