等式とは何か?理解を深める①
- 説明
-

学くんもずいぶん成長してきたね!!
このあたりで、算数という科目の大枠を教えておこうと思うよ。
文章題に比がでてきたとき、例えば4:5ならば、④とか⑤とかおくよね。
その後に何をしたら問題が解けるのかと言うと・・・
ずばり!
このような問題の最終目標は、「等式をつくる」ことなのです。
等式とは、「等号(=)」で結ばれた式のことだよ。④=600のような式が等式。
等式の例を他にもあげると、
④+100=⑤
とか
④×2-100=⑤+140
とか。等式は、「=(等号)」の左部分と右部分が等しい、ということを表しているんだ。
等式をつくれたら、あとは計算するだけで問題は解けるのです。

ふーん・・・そういうもの?どうしてでしょうか?

だって、最終的には「④はいくつか求めなさい」とか、そういう問題だよね。
④=200とかね。等式が最終目標なのは、当たり前じゃないかな?
それにね、ここは「どうして」って考えなくてもいい所だよ。
ゲームのルールみたいなものだと考えてね。この大事なルールは、とてもとても大事なんだけど、きちんと明言されることも、指導されることもないんだ。
学くんには、しっかりこのルールを覚えておいて欲しいんだ!
はい、しっかり覚えます!

うん。では、どんどん続きを教えていくよ!
小学生にとって「等号(=)」といえば250+15×6=
このような「これから計算するものの最後にあるもの」を思い浮かべがちだよね。
でも、等号とは、左右が等しいことを表す記号だ。例えば、1つ前の問題では、29+900=35
という等式がでてきたよね。
等式は、てんびんがつりあっているイメージで理解してみてね。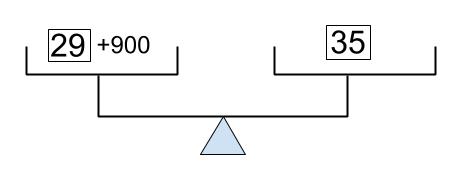

そして、等式は、今までたくさんやってきた線分図と同じものでもあるよ。
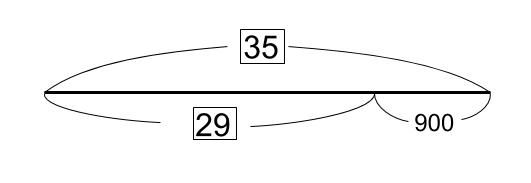

線分図と同じなら、線分図だけあればいい気がします・・・

ところがそれは絶対におススメできない。
線分図で解くととても複雑でめんどうだけど、式で処理すれば簡単っていうタイプの問題だってあるからね。もちろん逆もあるよ。
式処理だけではとても複雑でめんどうだけど、線分図で処理すれば簡単っていう問題もある。
式と図を同時進行で使っていくのが一番おススメだよ。
