2:消去算 てんびん(整数タイプ)
例題1
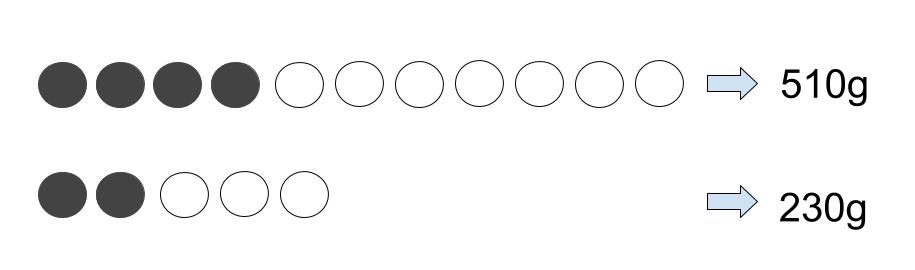
黒玉4個と白玉7個の合計の重さは510g、黒玉2個と白玉3個の合計の重さは230g
です。このとき、黒玉1個、白玉1個の重さはそれぞれ何gですか。
解説

あれ、線分図にできないよ。黒と白、どっちを長くかけばいいんだ?
どちらが重いかわからないよ。

線分図で整理するのが適さないのなら、他のやり方でやってみようね。

具体図かなあ。当てはめで調べるのは厳しそうだし・・・
具体図をかいてみますね。
えーっと・・・下図のようになりますね。

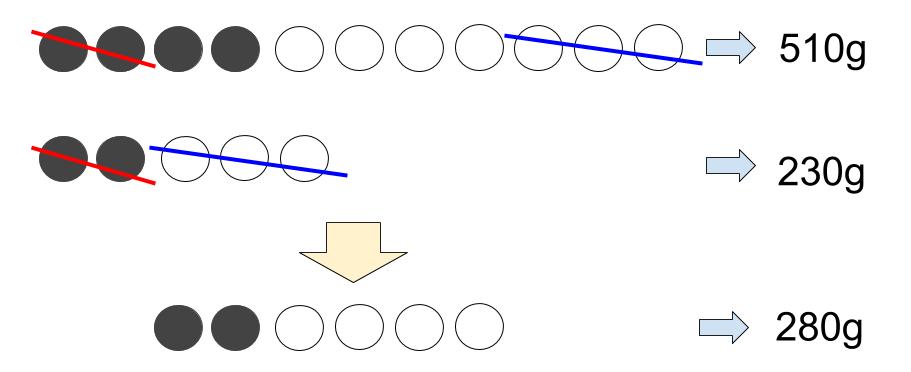
算数で着目することっていえば、和か差か、何倍か、だよね?

差をとると、
●●○○○○=280g
がわかります。

さらに差をとると、
〇=50(g)だ!!(280-230=50)
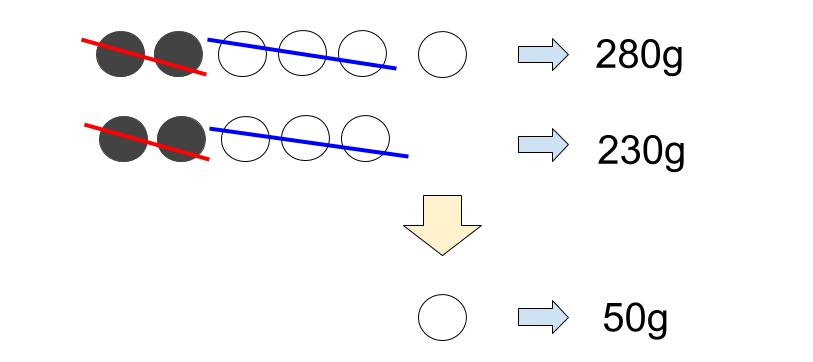

おっと!すごいね。白1個が50gで正解だ。

黒1個の重さは、あとは計算するだけですね!
●●○○○=230gだから、
●●+50×3=230g
●●=80g
よって、黒1個は40gです!求まりました!

正解だよ。本当にすごいね。まさか自力で解くとは・・すごいです。

今回のテーマは、「2回差を取れ!」ですね??

いや、そうではないんだ。
2回、3回と差を取っていくという解法もとても素晴らしいのだけど、
今回のテーマは「そろえて差をとって消す」なんだ。

????

学くんの解法は完璧でとても素晴らしかった。
ただし、問題の数値が変わると、かなり面倒になることもある。
だから、「何回も差をとればうまくいく」という視点を少し進化させるんだ。
今から教えるから、身につけてね。
※本質的にはまったく同じ解き方ですが、より洗練させます
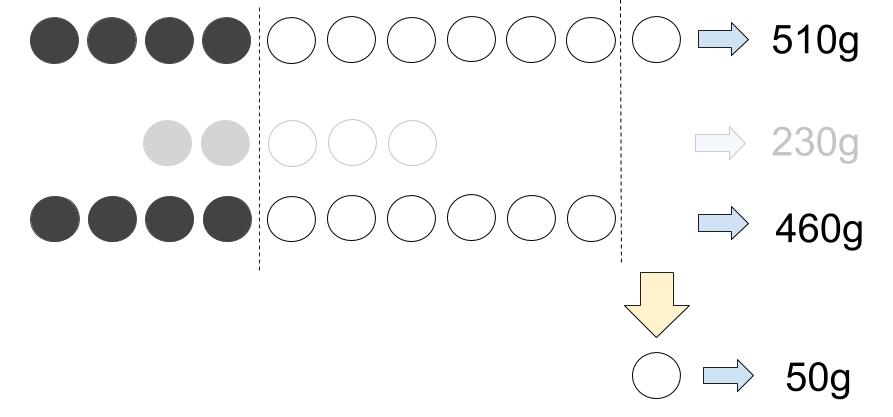
まず具体図なんだけども、下の図のように、黒は黒、白は白でそろえて書こうか。
こうすると差が見やすいでしょ。線分図の頭をそろえるようなものだね。
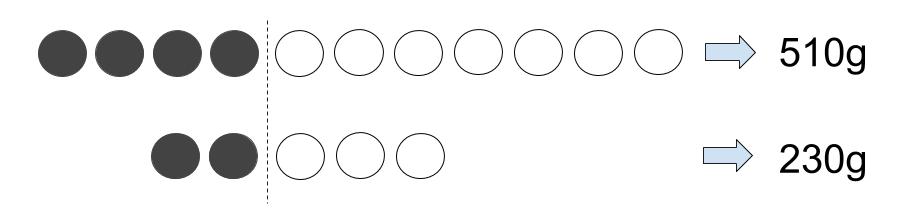

で、次なんだけど、
●●○○○=230gを2倍します。
つまり、
●●●●○○○○○○=460g
ということです。

●●○○○=230g
が2セットあるということですね。
230×2=460(g)ということか。


うん。ここがとても大事な考え方だからしかっり覚えてね。
あたりまえのことなんだけども、いざ自分1人でしっかり使いこなせないという子は多いよ。
で、なんのために2倍にしたのかっていうと、
もう1つの条件である
●●●●○○○○○○○=510g
と黒の個数をそろえるためなんだよ。
そろえてから差をとれば、黒が消えるでしょ。
白1個が、510-460=50(g)だって求まるんだ。
今回のテーマ「そろえて差をとって消す」ってこういこと。

なるほど。
差をとって消すためには、そろっていないと消えませんね。

うん、そこで個数をそろえるために、式全体を2倍、3倍のように、かけ算をすることがポイントになるんだよ。
今回は、先生の解き方と学くんの解き方は実質同じ解き方だったんだ。
2回ひいた学くんと、2倍したものを引いた先生、どちらも同じ解き方だ。
ただし、
「差をとって消す」ためには、「そろえる」という視点を持っていて欲しいんだ。
差を何回とっても、なかなかうまくいかないような問題だってあるからね。
先生のやり方を必ず覚えて欲しい。

わかりました。

このような計算方法を「消去算」とよぶんだ。名前の通り「消去」する計算方法だね。
この計算技術は、今後あらゆる問題で使うことになるよ。ものすごく大事だと覚えておいてね!
消去算とは、つまり連立方程式です。小学生においても、最重要の計算技術になります。
具体図から式へ

さて、●●●●○○○○○○○=510gのようにかきましたが、結構めんどうでしたね。
それに、●●●・・・と黒丸を20個かく必要がある問題がでてくることもあるでしょう。
ですから、式だけで上の解き方を表現してしまいましょう。
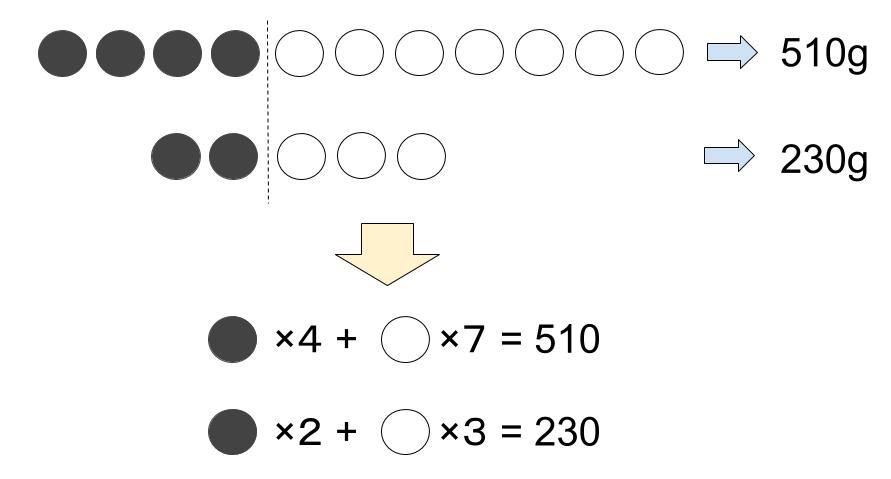

なるほど、これは楽ですね!

あるいは、黒玉1つを①gとします。もちろん、4つで④gです。
白玉1個はなんと表せるでしょうか。
黒玉1個の重さと白玉1個の重さは違うのですから、違う記号でそれを表現します。
白玉1つを1gとします。
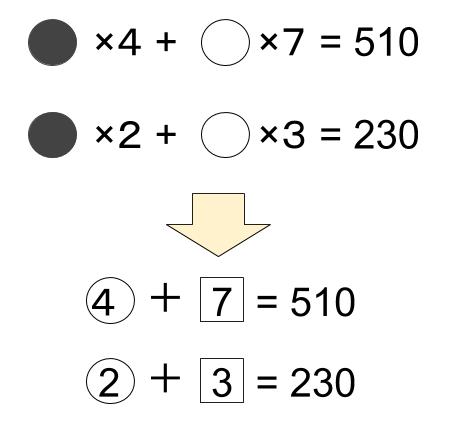

④+7=510
②+3=230
ここからは、先ほどの解き方と同じです。
下の式を2倍します。
②+3=230
を2倍して、
④+6=460
これと、もとのはじめの式との差をとります。
④+7=510
④+6=460
1=50
ずいぶん楽に解けますね!
求める方と逆を消しましょう、という指導をする教師も多いようです。
あまり気にすることではありません。
そろえやすい方をそろえることの方が圧倒的に有効です。
