【食塩水】導入・その2

さて、これから食塩水の問題を解いていきますが、食塩水の情報は下の図のようにまとめることをオススメします。

初心者のうちは、必ずやりましょう。

前ページの食塩水Ａを例に図示します。

Ａは水42gに食塩８ｇをとかした食塩水。
全体が50ｇで、濃さ16％です。　

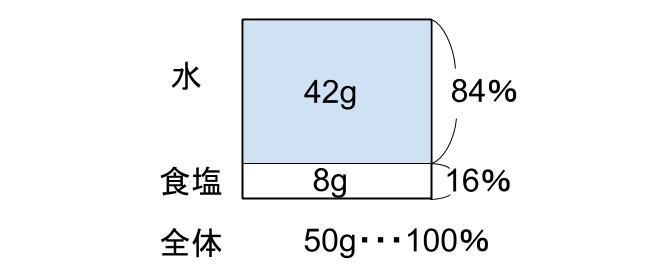
食塩が、水にとけないでビーカーの下にたまっているみたいですね。

そうだね。こういう図を模式図（もしきず）というよ。美術のようにかくことが目的じゃないからね。　　

全体50ｇが100％にあたります。　　
食塩が全体の16％ならば、残りの水は全体の84％　
食塩と水を合わせれば、全体（100％）になるのだから、あたりまえですね。　
16+84=100

食塩以外はすべて水ですからね。
演劇部の女子率が80％なら、男子率は20％っていうのと同じことですね。

そういうこと。

それで、「食塩は全体の16％」のところだけに、特別に名前をつけているのです。「食塩水の濃さ」と。

水のほうには名前はついていないんです。
※水の濃さとでも名付けておきましょうか。
このプリントでしか使わない、普通は使わない言葉ですから注意ですけれど！

「食塩水の濃さ」は、模式図の下の数値を分数にしてしまえば良いよ。

（濃さ）＝$\displaystyle \frac{食塩}{全体}$

だからね。

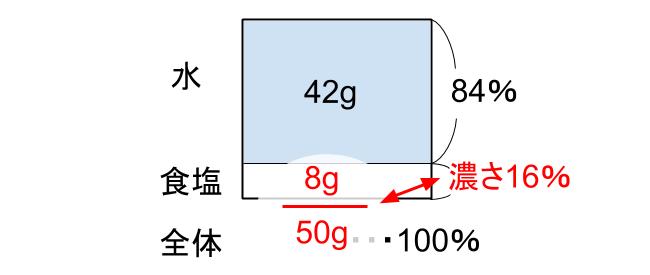
では、まずはこの模式図をかく練習からだ。
食塩水とは何か、濃さとは何か、これらをまずはきちんと暗記しないといけないからね。　

前ページの食塩水Ｂですね。
できました！

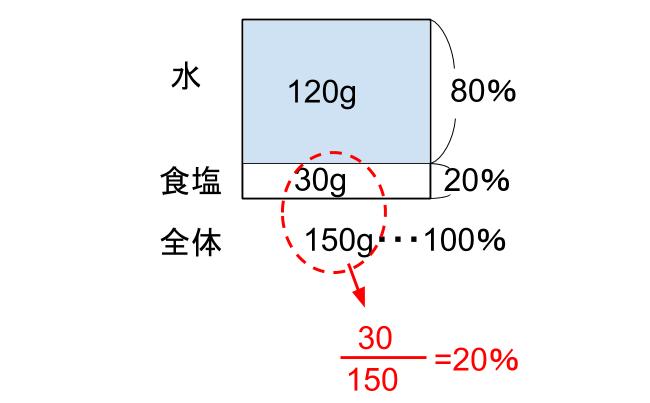
うん。ばっちりOKです！