【食塩水】食塩水の複数回移動・その1

さて、食塩水の面積図の解法はマスターしたかな？

はい！ばっちりです。
面積図があれば、食塩水の問題はなんでもこいっ！て感じです。

面積図はとてもうまく解けるから気持ちがいいよね。
でもね・・・
食塩水において、面積図があまり役に立たないときがあるんだ。

え？そうなの？
じゃあ、また何か新しい武器を教えてもらえるのかな。

　　
いや、もう新しい武器はないんだよ。

面積図が役に立たないときはどんなときか、そしてどのように解いていくのか。
例題をみていこう！

え？面積図がなんで役にたたないんだ？
まず
Ａ、７％の食塩水100g
Ｂ、９％の食塩水200g
を混ぜて・・・　濃さが、分数になるな・・・

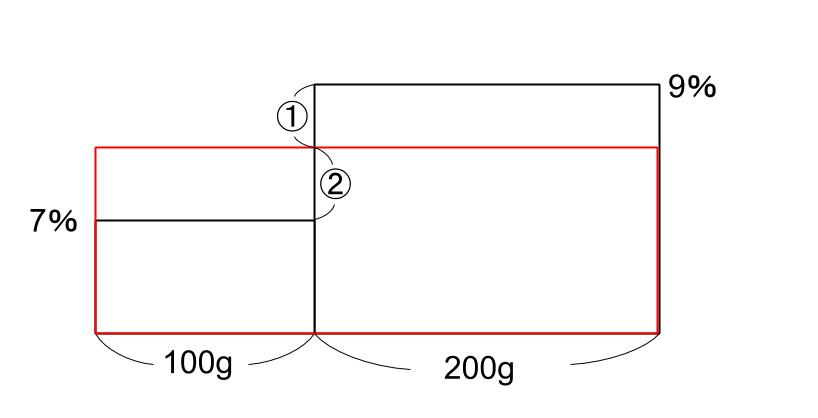
③＝２（％）

①＝\(\displaystyle \frac{2}{3}\) （％）

つまり、９－\(\displaystyle \frac{2}{3}\) =8\(\displaystyle \frac{1}{3}\) （％）

濃さが、分数・・・やだな・・・

うんＯＫＯＫ。
途中だけどストップ。

学くんは、面積図がきちんと習得できていてエライぞ！
このまま解き進めれば正解がでるんだ。それは間違いない。

でもね、この問題は面積図を使う必要はないんじゃないかな。

え？そうなの。
だって、うまく解けてるんでしょ。

でも、途中で濃さが分数になって、計算が面倒だっただろ。
この問題のコツは、
「ＡとＢをまぜた段階の食塩水の濃さなんて、求める必要がない」
ってことなんだよ。

え？そうなの？

学くんは、たくさん面積図の練習をしたんだよね。
それはとてもいいことなんだよ。

でもね、

「食塩水は必ず面積図を使う！」という決めつけをしてはダメなんだよ。

「食塩水において、面積図は万能ではない」と肝に銘じておいてね。

いくぞ！この問題はもっと初歩的に解くんだ。

Ａ：７％の食塩水100g にとけている食塩は７ｇ
Ｂ：９％の食塩水200g にとけている食塩は18ｇ
Ｃ：15％の食塩水100g にとけている食塩は15ｇ

Ａ、Ｂ、Ｃすべてまぜた食塩水の濃さが聞かれている。

すべてまぜると、
全体は、100+200+100=400（ｇ）
食塩は、７＋18+15=40（ｇ）

つまり、全体が400ｇで、とけている食塩は40ｇ。

つまり、濃さは10％
これで求まった。

あ！なるほど・・・面積図なんていらないんだな・・・

面積図は必ずマスターしておかないといけない道具だ。
面積図がないと解けない問題があることも見てきたよね。
でもね、今後は必ずしもいつもどこでも面積図、という考えは捨てて欲しい。

ところで、食塩水の模式図からはじめて、面積図まで学習してきたわけだけど、
これからは食塩水の問題を解くときの図として、もっと簡略化した図も使っていこうと思う。

例えば、
Ｂ：９％の食塩水200g にとけている食塩は18ｇ
これを下図のように表す。

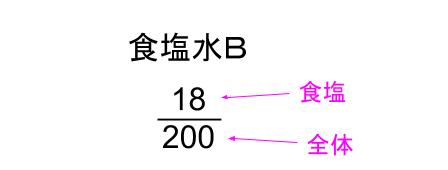
分数のように見えるけど、分数ではないからね。
これは食塩水の簡易表示だからね。

Ａ：７％の食塩水100g にとけている食塩は７ｇ
Ｂ：９％の食塩水200g にとけている食塩は18ｇ
Ｃ：15％の食塩水100g にとけている食塩は15ｇ

これらＡ、Ｂ、Ｃをまぜると
全体が400ｇでとけている食塩は40ｇの食塩水になる。
これは下図のように表せる

くりかえすけど、分数じゃないからね。
分母の通分とかしないでね。そもそも分母でもないんだからね。

この図は、食塩水を簡略に表現できるから、たくさん移動したりまぜ合わせしたりする問題を整理するときに適しているんだ。

面積図を使うまでもないような問題を整理するときの図と思ってくれてもいい。

ただし、「水」の情報がない。だからこそ、「水」も大事なんだな、と理解をしている人でないと、落とし穴にはまることもある。

まとめると、
・利点は、図より簡単に（時間をかけずに）かけること。
・弱点は、水の情報がないこと。
きちんとわかった上で使っていくんだよ。