比は、問題を解くときは、３：５のようには使いません。③と⑤のように使います。これこそが、算数における最重要の計算テクニックとなります。本質的には、１次方程式を学び始めることとなります。比＝線分図の山を指します。
比の使用方法・仮の値で考える
- 例題１
- Ａの所持金はＢの所持金の４倍で、2人の所持金の和が600円のとき、Ａの所持金はいくらですか。
- 解説
-
基礎の基礎の確認なんだけど、大丈夫かな？
はい、ずい分前に身につけた話ですこれは。４年生でやったかな。
こんな線分図です。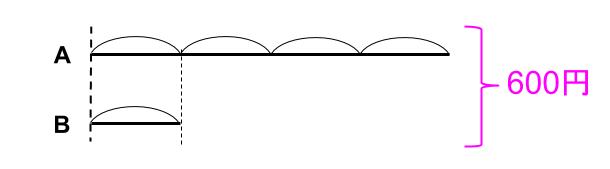
合計の５山が600円なので、1山120円です。
Ｂが120円、
Ａは４山だから、120×４＝480円うん、正解です。
この問題を塾で習うのは、比や割合を習うよりかなり前の時期、4年生で習うことが多い。
しかし、これだって比の問題だよね。そうですね、4倍っていうところ。
Ａ：Ｂ＝4：１
っていうことですからね。そういうことです。
前にも教えた通りだけど、線分図は山をかかないで下のように書いてしまうのが楽だね。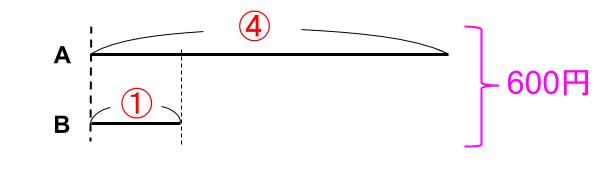
結局「比」とは、線分図で何山あるのかと同じことを表しているんだ。
とても簡単な問題ならば、線分図を省略して解いたってかまわないよ。
- 例題２
- 800円をＡ：Ｂが11：5になるように分けました。Ａはいくらもらいましたか。
- 解説
-
簡単でしょ。
線分図をかかなくても解けるんじゃないかな？Ａは⑪、Ｂは⑤もらいます。
2人の和、⑯＝800円なので
①＝50円です。
Ａは⑪もらったので、50×11＝550円大正解！
問題の中で比を見たら、⑪とか⑤とするくせをつけようね！文章題を解いていくときに、11：５のような比そのままの表記をしても先に進まないからね！
ちなみにこのように比にしたがって分けることを、比例配分といいます。
- 例題３
- おこづかいを、弟が兄の \(\displaystyle \frac{2}{3}\) となるように分けたところ、兄は弟より400円多くもらいました。弟がもらったおこづかいはいくらでしたか。
- 解説
-
「比」がない問題かな・・・？
「比」はないけれど、「比」と同じもの「分数」があるよね。
ああ、そうですね。
弟が兄の \(\displaystyle \frac{2}{3}\) とは、
弟と兄のおこづかいの比が、
２：３
ということだ。その通り。
弟と兄のおこづかいの比が、
２：３
だから、
弟が②円、
兄が③円
もらったとすれば、
2人の差は①＝400円だから、
弟がもらったおこづかいは②＝800円！正解！