規則性
等差数列
解説

このような問題のジャンルを「数表」と言うこともあります。

数の表ですね、はい。

タイトルは数表でもなんでもいいのですが、この問題を見て頭に浮かんで欲しいことは「等差数列」なんですよ。

えっと・・・?
どこに等差数列があるの??

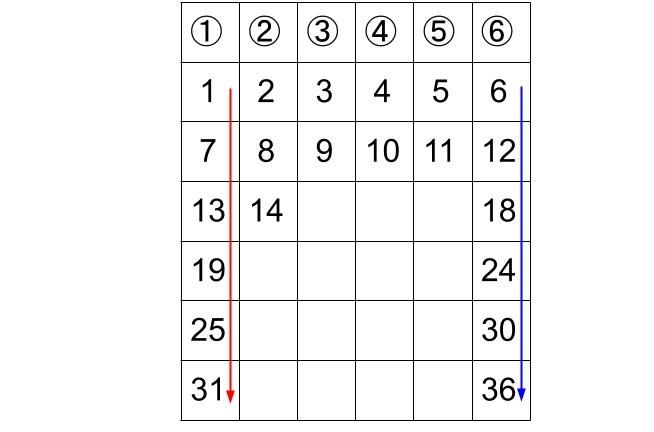
たてに見るのですよ。
6ずつ増える等差数列が、6本あります。
例えば、
6列目の数は、6の倍数の列。
1列目の数は、「6の倍数+1」の列。

あ!そうか。
6で割ったときのあまりは、1~5と0の全6種類。
これが各列に並んでいるんですね。

はい、では問題を解きましょう。
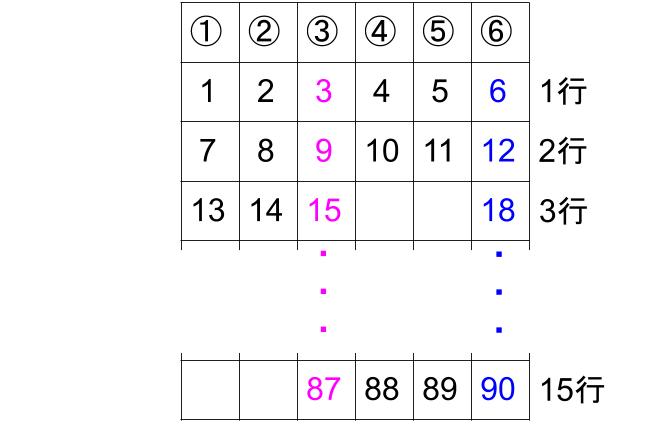
(1)15行3列の数

3列の数は、
3、9、15、21、27、33、39、・・・
という等差数列だから、15行の数は、15番目の数。
3+6×14=87
求まりました。
87です。

正解です。
15行6列の数が、
15番目の6の倍数、90であることから解いてもよいですね。
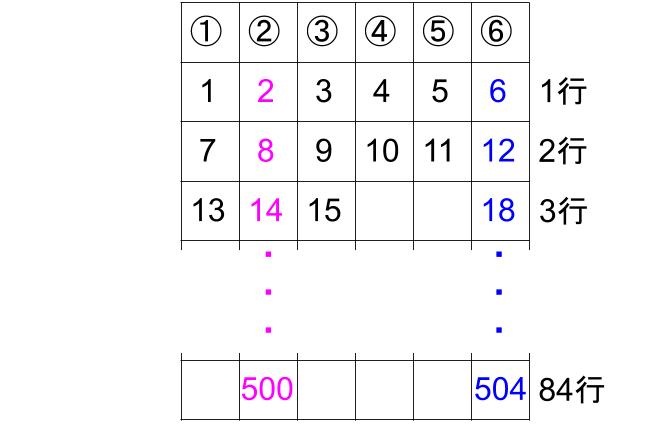
(2)500は何行何列か

500÷6=83あまり2
あまり2だから、2列の数だ。
あとは何行目か。
83行目か84行目な気がする・・・

そうだね。
500と同じ行にある6の倍数を使うのがおススメかな。

504だ。
504=6×84
ということは84行目だ!
500は、84行2列にあります!

正解です。
もちろん、植木算的に等差数列の処理をして解いても良いですよ。