等差数列・その５

えっと・・・
何だこの問題・・・
わからないな・・・

差はいくつの等差数列なのかというと・・・？

３ですね。

つまり、この数列に出てくる数は、
２
２＋３
２＋３＋３
２＋３＋３＋３
２＋３＋３＋３＋３
と続いていくから・・・

あ、なるほど。
３で割ると２余る数ですね。

ア＝３、イ＝２です。

はい、正解です。
そういうことです。
そして、「３で割ると２余る数」とは言いかえると
「３の倍数＋２」と言うことです。
さらに言いかえるならば、
「３×整数＋２」

このように等差数列とは、「アで割るとイ余る数」の集まりなのです。
このような理解も必ずしておいてください。

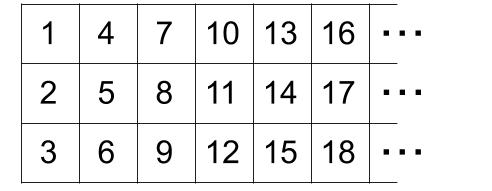
ここで、整数を下の表のように３段に並べます。

３本の等差数列ができました。

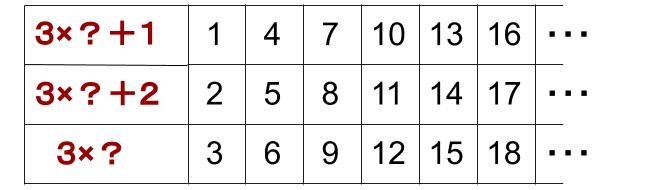
上から順に、
「３で割ると１余る数」の列
「３で割ると２余る数」の列
「３で割ると割り切れる数（あまり０）」の列
となります。

この表を使って、等差数列を簡単に処理することができます。
例えば次の例題です。

もちろん、表を使うまでもなく３秒で答えが出せますね。

２＋３×49＝149
答えは149です。

正解です。

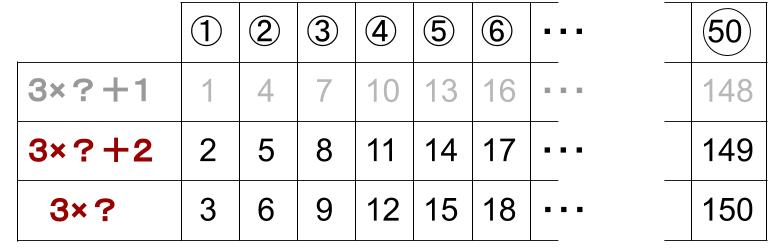
別解は、「３の倍数の列」を使います。
50番目の３の倍数は、
50×３＝150
と極めて簡単に求まります。

求める値は「３×？＋２」の数列の50番目なので、149です。

なるほど。
「植木算」の要素がなくなりましたね。

そうなんです。

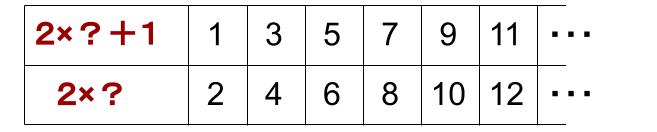
さて、同じように整数を２で割ったときのあまりによる分類は下図のようになります。

これには、「奇数」と「偶数」という名前がつけられています。

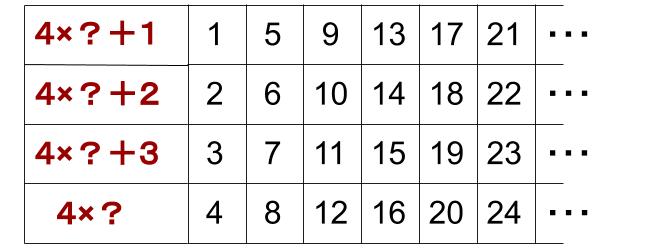
同様に、整数を４で割ったときのあまりによる分類は下図です。

以下、同じように、５で割ったとき、６で割ったとき・・・と無数の分類が可能です。
このような数表がそのまま出題されることも非常に多いので、頭に入れておきましょう。