等差数列・その２

４ずつ増える規則ですね。
10番目までをかき出します。

１、５、９、13、17、21、25、29、33、37

この10個の和を求めればいい。
ちょっと面倒ですけど・・・

そうだね。ちょっと面倒だ。
でも、簡単に計算できるよね。

はい。
１＋５＋９＋13＋17＋21＋25＋29＋33＋37=190

求まりました。190です。

はい、正解です。

10個だからなんとかなりましたけど・・・
50個とかの和を求めろって言われたら無理ですよ。

そうだね。
「等差数列の和」について、とても簡単に求められる方法があるんです。
今から、それを教えますよ。

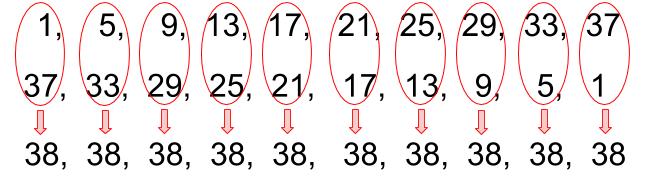
まず、下図のように、数列を逆に並べたものをかきます。

ここにある20個の数の和は、今求めたい和の２倍です。

そうですね。同じ数列が２個あるのですから。

では行きます！
20個の数の和を求めますが、まずは上下に並んだ数の和をとります。
すべて38になります！

あ！
本当だ。
不思議だな・・・

さて、38が10個できたわけだ。
だから、その和は、
38×10＝380
これは今求めたい和の２倍なのだから・・・

380÷２＝190
あ！さっきの答えと同じだ！
10個かき出してから全部足した値と同じ。
魔法みたいですね。

まとめておくよ。
等差数列のN個の数の和の求め方だ。

その数列の「はじめ」と「最後」を足します。
この値が、N個できるので、N倍します。
最後に２で割ればOKです。

（はじめ＋最後）×個数÷２＝等差数列の和

ということです。

簡単ですね。