2・つるかめ算 面積図
具体図を発展させた図が面積図です。
抽象度が高まりますので、お子さまの成長段階に注意して指導しましょう。
理解できない場合、急ぐ必要はありません。どうしても無理なようなら、数か月あとに再指導しましょう。

つるかめ算はばっちりかな?

はい、もう具体図も上手にかけますよ。

それはよかったよ。
お勉強はどんどん進むからね、前のことがわからないと次のお勉強ができないから。

どんどん新しいことが知りたいです!

よし、その意気だ。
今日はまた、つるかめ算を扱うよ。
今日は具体図から発展させて、「面積図」というものを学ぶよ!
例題2
ツルとカメがあわせて13ひき(羽)います。足の数はぜんぶで34本です。
ツルは何羽いますか。カメは何ひきいますか。
※ツル1羽の足は2本、カメ1ひきの足は4本ですよ。

以前に扱った例題1とほとんど同じ問題なんだけどね。
「もし全部ツルだったら」はこのような具体図であらわせたよね。
このとき、足の総数はもちろん、13×2=26だね。


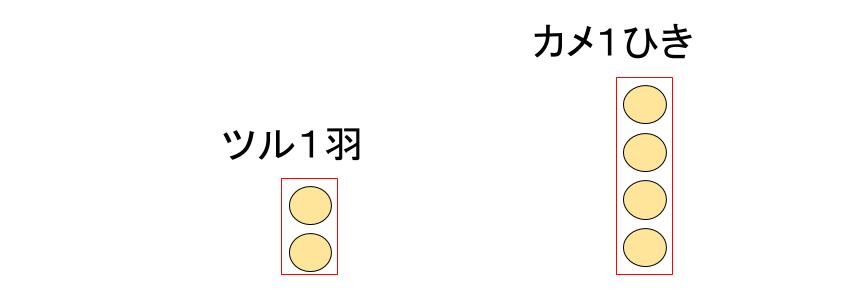
ところで下の図のようにかくこともできる。
ツル1羽が足2本持っていることや、カメ1ひきが足4本持っていることを表す図だ。

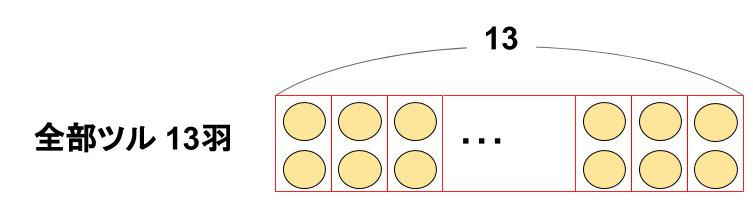
そして、ツルが13羽いる図は下図のようになる。

ちなみに、この問題の答えはツルが9、カメが4なのだけど、下図のようになるよ。
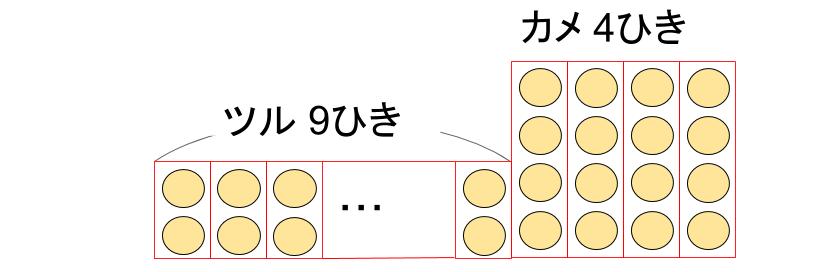

○1つが足1本を表しているわけですが、この○の総数は、かけ算で求めることができます。
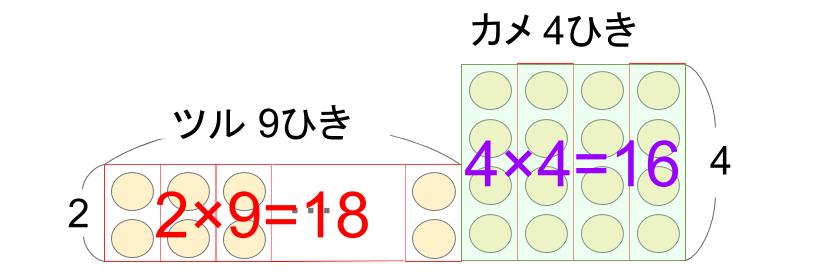

これはつまり、「長方形の面積が足の数を表している」とも言えます。
○をたくさんかくのはさすがに面倒なので、今後は省略しましょうね。
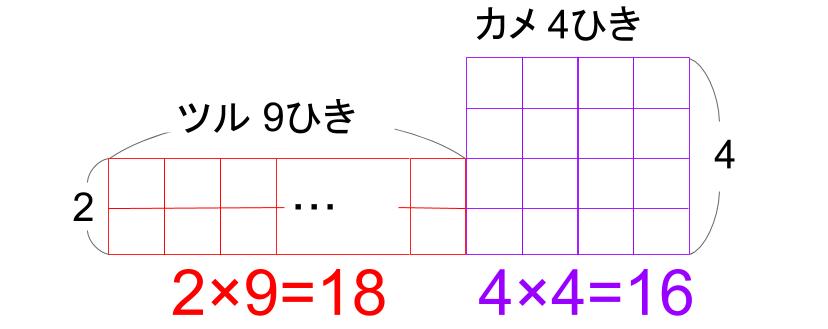

さっきも言ったけども、「面積が足の数を表している」ね。
このように、面積を使って数量を表す方法を面積図と言うんだ。
面積図と相性の良い問題とそうでない問題があるからね。
まずは「つるかめ算は面積図で解くと楽」
重要な経験として覚えておこう!
つるかめ算は、最終的には面積図で身につけましょう。
いずれは、小数・分数もでてきます。具体図で、整数しか取り扱えないのでは困ることもあります。
例題3
タコとイカがあわせて20ひきいます。足の数は全部で186本です。
タコは何ひきいますか。イカは何ひきいますか。
※タコ1ひきの足は8本、イカ1ひきの足は10本ですよ。
※正しくは1はい、2はいと数えますが、「ひき」とします。

では、面積図で解く練習をしてみよう。

えっと、タコは足が8、イカは足が10・・・
図にするの面倒ですね。

8とか10とか、まともにかく必要はないよ。
例えばタコ1ひきは、下図のように省略すればいい。
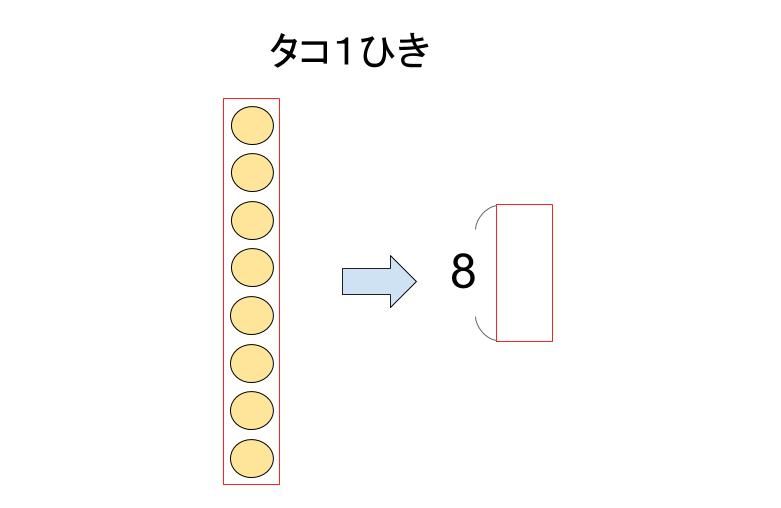

なるほど!
じゃあ、タコが何匹か、イカが何匹かいる図はこんなですね。
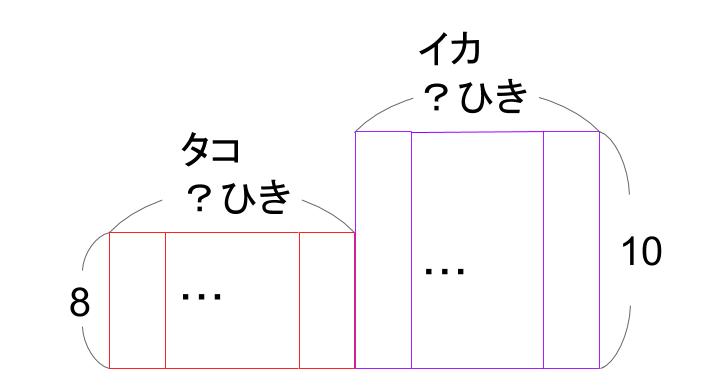

うん、いい感じですね。
全部で20ひき、足の合計は186という情報も図にいれようね。
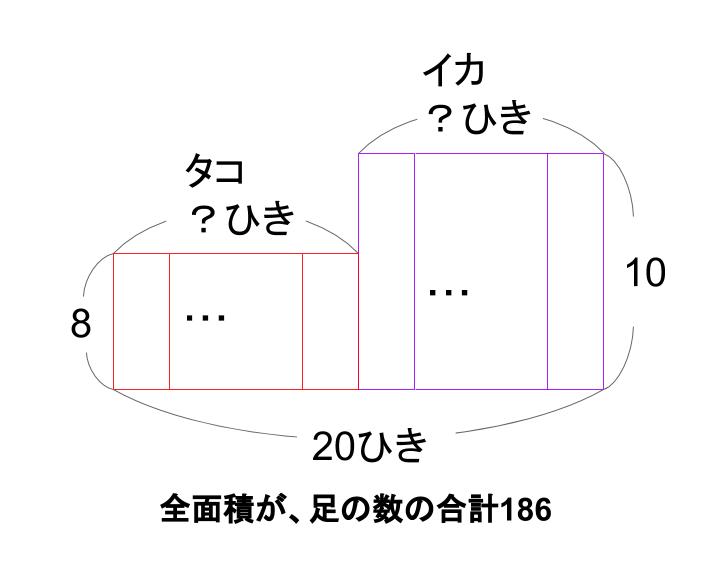

あとは図形の問題を解くのと同じだよ。
問題を解くときは、図がごちゃごちゃしていると解きにくい。下図のようにかいてしまってOKだよ。
もちろんこの図が何を意味しているのか、理解している人だけが使っていい図だぞ。
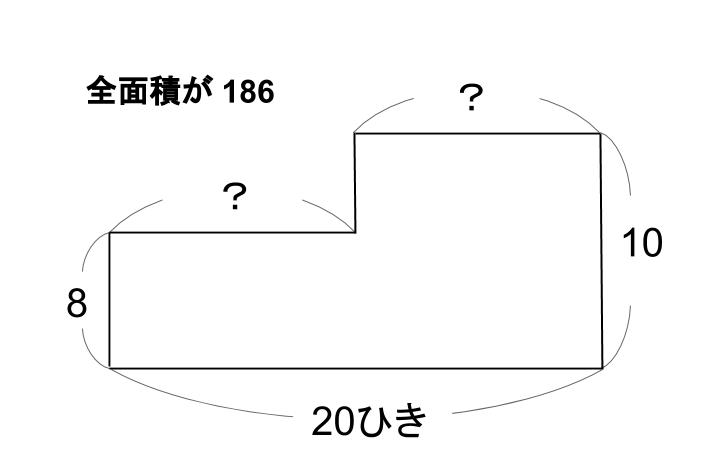

図形の問題を解くのと同じですね。
8×20=160・・・ピンク色の面積
186-160=26・・・クリーム色の面積
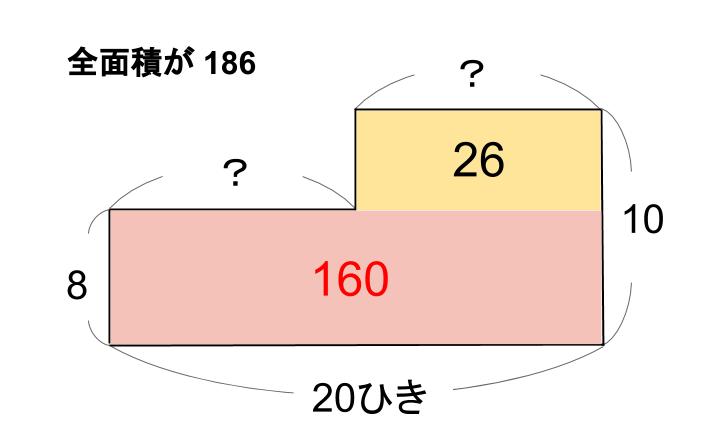

クリーム色の長方形のたての長さは、10-8=2
だから、26÷2=13


これは、イカが13ひきということ。
だから、タコは、20-13=7
求まりました。
タコは7ひきです。
確かめをすると、
タコ7ひきで、足は、8×7=56
イカ13ひきで、足は、10×13=130
合計は、56+130=186
間違いないですね!

確かめもバッチリだね!問題の条件と合っているかを確かめるのは文章題では重要なことだよ。
特に家庭学習時には必ずやらなくてはいけないよ。
