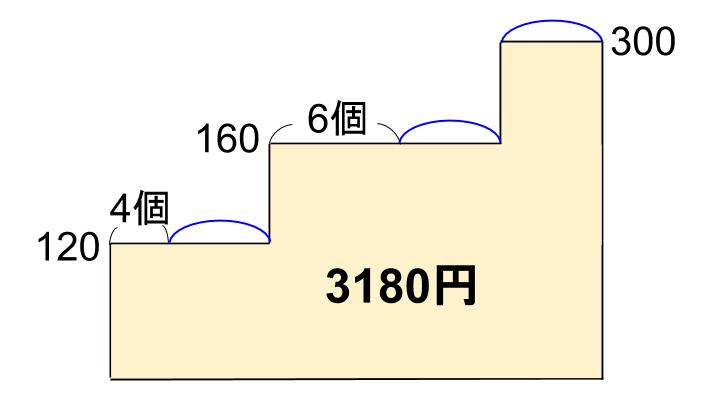
差集め
個数を逆にする
例題1
3つの商品A、B、Cがあり、1個の値段はそれぞれ120円、160円、300円です。
A、B、Cをそれぞれ何個ずつか買って、全部で3180円はらいました。
もしAとBの個数を取り換えて買うと3100円になり、もしAとCの個数を取り換えて買うと3900円になります。Aを何個買いましたか。
解説

商品が3つありますね・・・
図示がたいへんそうですね。

そうだね。
基本的なことは図なしで処理できてしまうのが理想だな。
まず、
AとBの個数を取り換えて買うと80円安くなった。
ここからAとBの個数の差が求められるよね。
もう図なしで求められるかな?

A1個の値段は120円
B1個の値段は160円
だから、
80÷(160-120)=2
差は2個ですね。
「実際」の方が「もしも」よりも高いのだから、実際の方が値段の高いBの個数が多い。
AよりBが2個多い。

そうだね。
で、せっかくわかった事実はメモしておくべきだよね。
下の線分図のようにメモしておこう。
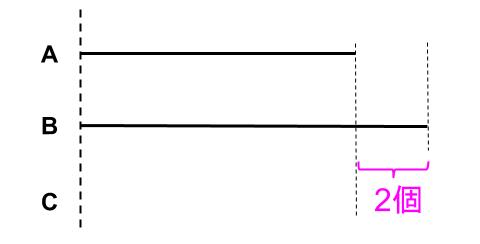

AとCの個数を取り換えて買うと720円高くなる。
A1個の値段は120円
C1個の値段は300円
だから、
720÷(300-120)=4
差は4個ですね。
「実際」の方が「もしも」より安いのだから、実際の方が値段の安いAの個数が多い。
CよりAが4個多い。
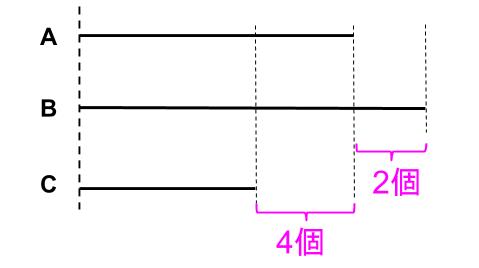

面積図にかきなおさなくても、この線分図でとけるでしょ。

A1個の値段は120円だから、4個で480円
B1個の値段は160円だから、6個で960円
あとは、A、B、Cを同じ個数ずつ買った。
3180-(480+960)=1740(円)
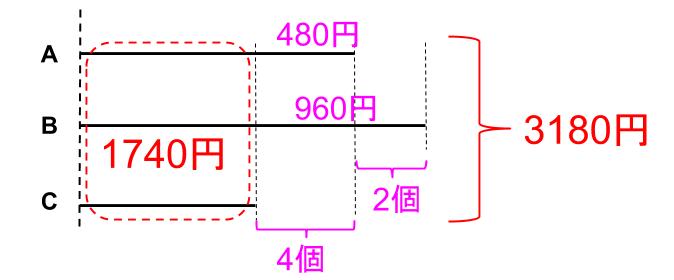

A1個の値段は120円
B1個の値段は160円
C1個の値段は300円
A、B、Cを同じ個数ずつ買って1740円なので、
1740÷(120+160+300)=3
3個ずつ買った。
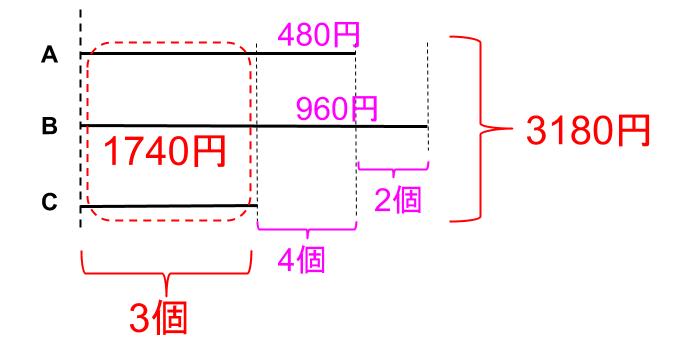

よって、
Aは7個、Bは9個、Cは3個買った。
求める答えは、Aの買った個数なので、7個!

正解です。
線分図が、「個数」を表す図だったので、
これに金額をあわせて書く上の解き方では、混乱がおきる可能性があります。
だから、必要ならば、個数がわかった時点で、
面積図を新しくかいて解くのがていねいではあります。