差を集める
弁償算(マイナスのつるかめ算)
例題1
太郎君はコップを200個運ぶ仕事をしました。1個につき50円もらえますが、運ぶと中で割れてしまったコップについては50円もらえないうえ、1つにつき30円払わなければなりません。太郎君はこの仕事で8960円もらいました。うまく運んだコップは何個ですか。
解説

こんなお手伝い嫌ですよ。

そうだね、たくさんこわしたら罰金もたくさんだものね。
ところで解けそう?

どうかな・・・・

まず199個うまく運んだとする。
最後の1個なんだけど、
ア うまく運べた
イ 割ってしまった
アとイで、もらえる金額の差を考えてみよう。
199個うまく運んで、それで仕事終了ならばいくらもらえるかな?

50×199=19950(円)です。

うん。次に、最後の1個を運ぶのだけど
ア うまく運べた
イ 割ってしまった
アとイで、もらえる金額の差はどうなるかな?

アだと、19950+50=20000
イだと、19950-30=19920
80円の差ですね。
「50円もらえる」と「30円引かれる」の差は80円になります!

その通り。
線分図でこの80円の差を理解しておこうね。
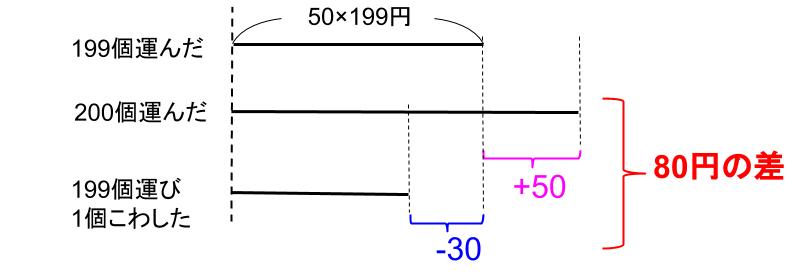

で。
198個運んで2個こわしたら、
197個運んで3個こわしたら・・・どうなるだろう?

1個こわして80円もらえる額が少なくなったから・・・
2個こわしたら、160円、
3個こわしたら、240円
もらえる額が少なくなると思います。

その通りです。今回は完璧に運んだときと比べて、いくら少ない?

10000-8960=1040、1040円少ないです。
だから、1040÷80=13、13個こわしました!うまく運んだのは200-13=187個です!

確かめをしてみようか。

50×187-30×13=9350-390=8960
はい、うまくいっています。

うん。矛盾がないことも確かめられたね。
ところで、今解いてきたことの全体像を、目て見て理解を深めておこう。
具体図だ。
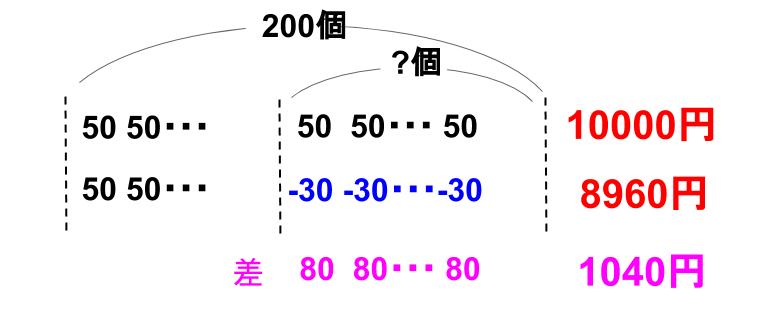

差の80円が集まって、全体の差、1040円になる。
1040÷80=13
こわしたのは13個。
わかりやすいですね。

そう、差を集めている解き方だ。
つるかめ算と似ていることはすぐにわかるでしょう。
しかし、この問題を面積図で、つるかめ算のように解くことはできないんだ。
具体図で差を集めて解こうね。
