【和と差】差一定・その1

どう？この問題解けそう？

具体図か線分図か、あてはめで探すか、ですよね・・・

うん、そうだね。

図にまとめられそうにないです。
あてはめてみます。

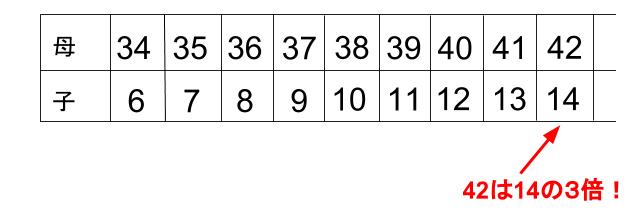
ようやく見つかりました・・・
６才の子が14才になった。８年後です。

正解です！
立派だよ。あてはめで答えがだせるのはすごく大事なことだよ。
そして、せっかく書き出したんだから、この表に何かヒントが隠れていないか探してみよう。

ヒント？
何も見えないし、どこを見たらいいかもわかりません。

じゃあ、ヒントを探すためのヒントをだすよ。
算数では「和」か「差」か「～倍」のどれかに着目することがほとんどなんだ。　
３択だよ。

あ！差だ！
母－子の差が、全部28になっています！

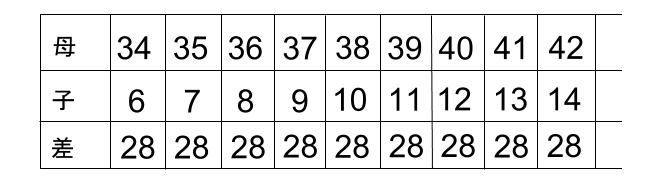
その通り。
では、この事実をどう使えば、この問題が解けるのか・・・

どんなときでも差は28・・・
差を表すのに便利なのは線分図ですかね。

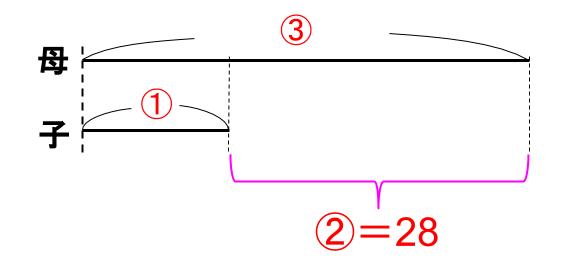
②＝28だから、①＝14
つまり、子が14才、母が42才のときに３倍になる。
これは８年後だ！

正解ですね。
とても上手に線分図を使えましたね。

これは、なかなか気づけないですよ。
どうやったら気づけるんですかね？

いい質問するね、学くん。
今回のように、地道な作業をすることで気づける道が開けるわけだ。

毎回毎回やるんですか？
それに、必ず気づけるわけでもなさそうだし・・・（嫌だなあ）

分からないときに、地道に作業をするのは大事なことだ。
それを通じてしか算数の真の仕組みは見えてこないからね。

でもね、すべての問題を、毎回毎回地道に調べて欲しいとは思っていないよ。
基本の定番問題は、一度しっかり考える経験を積んで、その後は解法を暗記
してしまってほしい。

解法は暗記しちゃダメだって聞いたことがある気がしますけど・・・

「解き方の意味がまったくわからないもの」を何も考えずに、暗記してはダメだよ。ちょっとひねられただけでまったく解けなくなるからね。

ところが、「一度本当にわかったこと」って、結局は暗記してしまうでしょ。覚えるなって言われたって、覚えてしまうよ。
定番の基本問題は、一度きちんと理解をして、自然と暗記するくらい練習を積むべきなのです。

ふーん。そうかも。

「差に着目」してみよう！
という解くための指針も暗記してしまって何の問題もない。それどころか、暗記しておくべきだ。

難しい問題に出会ったとして、そのときどのような頭の使い方をするべきかというと、今まで使ってきた道具がこの問題にも使えるだろうか、という検証をするんだよ。どの道具が有効利用できるかはわからないから、いろいろ試してみるんだ。しかし、そもそも道具を持っていないと、まったく手も足もでない、ということになってしまう。

では、まずは道具をたくさん持たないといけないんだね。

その通り。今は、様々な基本の定番問題に触れることで、算数における「大切な考え方の型」＝「道具」を増やしている時期なんだ。

確かに、次にこの問題に出会ったら、差が常に等しいということは覚えていると思う。覚えやすいもの。

一度書き出して実感もしているから、なおさらだよね。

いずれは、今回のような年齢ではない問題でも、「差が常に等しい」という仕組みが隠れている問題と出会うことになる。
そのとき、「差が常に等しい」という仕組みが見抜けるようになることが目標なんだよ。

さて、線分図の利用について、もう少し見ておこう。

線分図は差を表現することにすぐれている図です。

だからこそ、頭をそろえて線分図をかくことで差を見やすくしているわけです。
だから、現在の線分図をかくなら下図になりますね。

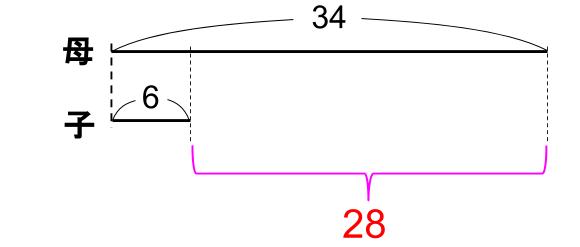
そして何年か経ちます。

1年後も２年後も、何年後であっても「差28」

つまり、はじめにかいた線分図の「差28」を保つべきですから、
線分図は左に伸ばすべきなのです。

そして、子が①才、母が③才のときを求めるのですから下図です。

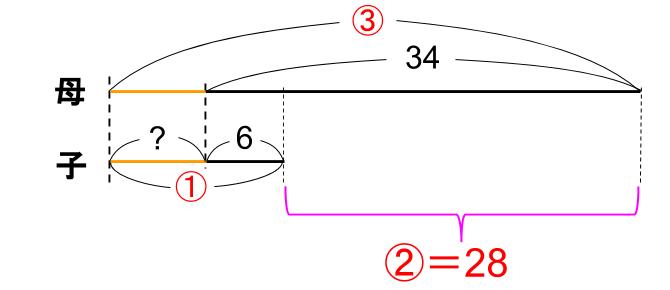
この作図をすることで「差が変化しないこと気づく」ということはまれでしょう。むしろ、「差が変化しないときに、線分図はどうかくべきか」という知識です

「差が変化しない」つまり「差一定」は、問題文をよんですぐにわかるようになっておきましょう。