【和と差】線分図と○倍・その2

　　　　　　　　　　　　　　　　
さっきと似てますね。線分図をかいてみます！

　　
えっと、和は12山だから、・・・
1320÷12=110　
１山が110円
つまり、Ｂは110円だ！
Ａは、110×11＝1210
1210円です。

お見事！！線分図にずいぶん慣れてきたね。
　　　
ところで、11山をかくの、たいへんだったでしょ。

別に・・・たいへんでもないかな・・・

「30倍」って問題が出たら、30山かく？
嫌でしょ？

う、う・・確かに・・・嫌ですね。

それにどう？改めてさっきの線分図を見てみて。
ＡがＢの何倍なのか、パッとみて分かる？

11山かいたよ、というメモがないと、パッとみて分からないよね。

確かに・・・毎回山を数えるのも嫌ですね。

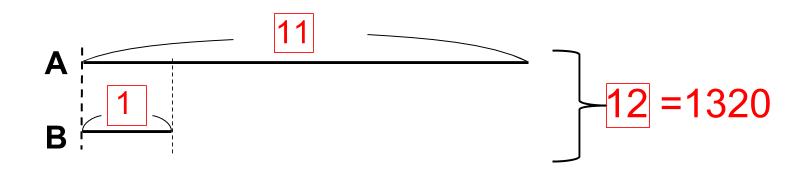
これって下のようにかくことにしましょう。

Ａの線分を11個に割ったというメモをつければ、実際に図を11個に割らなくてもいいでしょ。
それに、Ａの長さを律儀にＢの11倍の長さでかかなくともよいです。

ああ、なるほど。
これは図をかくのが楽ですね。
全部で12山で、1320円
1山が110円。

さて突然なんだけども今まで、1山と読んできたものを、①とするよ。
つまり、先ほどの図はこうなる。

⑫＝1320円だから、①＝120円

えっと・・・？なんで①にするのかな？

１山って書きにくいし、見にくいから。
ただそれだけだよ。

実を言うと、①でなくて、１ でもいい。
１だって、これから先どんどん使っていくよ。
例えば下図のように。

大事なことは、①とか１は、線分図における１山分を表していると理解すること。

１山がどれくらいの値なのかは不明だよね。
だから、①や１という、実際の値ではない仮の数値を使うんです。
　　　　　　
①としないで１とすると、Ｂが１円、Ａが11円のような勘違いが起きやすい。

①は、１山を表しているのであって、１円という実際の値ではない。
本当の値ではなくて、「仮の値」なんです。

わかりました。