相当算・基礎
差相当
例題1
父の持っているお金の \(\displaystyle \frac{1}{3}\) を兄、\(\displaystyle \frac{1}{4}\) を弟がもらいました。2人のもらった金額の差が150円のとき、はじめに父の持っていたお金はいくらですか。
解説

図にすると・・・
あれ?
こんな感じかな・・・
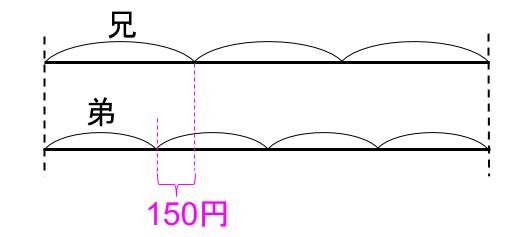

そうですね。
間違ってはいませんよ。

兄は \(\displaystyle \frac{1}{3}\) で、
弟は \(\displaystyle \frac{1}{4}\) だから、
その差は、
\(\displaystyle \frac{1}{3}\) -\(\displaystyle \frac{1}{4}\) = \(\displaystyle \frac{1}{12}\)
これが、150円ってことかな。
父のはじめの \(\displaystyle \frac{1}{12}\) が150円
つまり、父のはじめは、150×12=1800円

はい。正解です。
間違いではないけれど、上の図はすごく役に立つ図でもなかったね。

別解を紹介します。
父のはじめの線分図を、3等分、また4等分したいわけだ。
このようなときは、3と4の最小公倍数12を使う。
12等分するといい。
もちろん、12山にわけた図ではなくて、⑫としてしまえばよいよ。
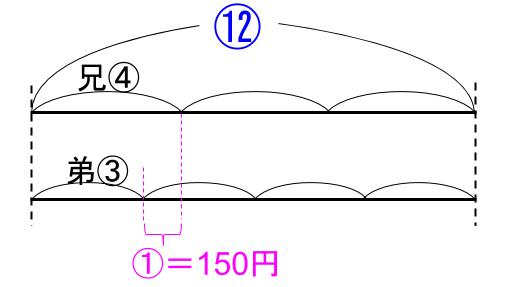

兄は、⑫の \(\displaystyle \frac{1}{3}\) で④
弟は、⑫の \(\displaystyle \frac{1}{4}\) で③
その差①が150円
⑫=1800円
なるほど!

これは「連比」という解き方の一種になります。
くわしくはまた「比」の分野で学習することになりますが、現時点で使いこなせるならどんどん使っていきましょう。
